Question

15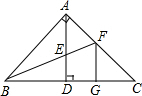．如图，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC，BF平分∠ABC，交AD于E，FG∥AD．
（1）求证：AE=AF；
（2）试判断DE、FG与CD的数量关系并证明你的结论．

Answer 1

分析 （1）根据已知条件得到∠ABF+∠AFB=∠CBF+∠BED=90°，由BF平分∠ABC得到∴∠AFB=∠BED，根据对顶角相等得到∠AEF=∠AFB，根据等角对等边得到结论．
（2）根据角平分线的性质得出AF=FG，进而得出AE=FG，证得△ADC是等腰直角三角形，得出AD=DC，
即可证得ED+FG=DC．

解答 （1）证明：∵∠BAC=90°，AD⊥BC，
∴∠ABF+∠AFB=∠CBF+∠BED=90°，
∵BF平分∠ABC，
∴∠ABF=∠CBF，
∴∠AFB=∠BED=∠AEF，
∴AE=AF；
（2）解：DE+FG=CD，
证明：∵AD⊥BC，FG∥AD．
∴FG⊥BC，
∵BF平分∠ABC，∠BAC=90°，
∴AF=FG，
∵AE=AF，
∴AE=FG，
∵在△ABC中，∠BAC=90°，AB=AC，
∴∠C=45°，
∵AD⊥BC，
∴∠DAC=45°，
∴AD=DC，
∵AE+ED=DC，
∴ED+FG=DC．

点评 此题考查了等腰三角形的性质、直角三角形的性质以及角平分线的性质，熟练掌握等腰三角形的性质是解题的关键．