��Ŀ����
6������֤���н��۵���ȷ�ԣ��ٷ���x-$\frac{1}{x}$=2-$\frac{1}{2}$�ĸ���x1=2��x2=-$\frac{1}{2}$��
�ڷ���x-$\frac{1}{x}$=3һ$\frac{1}{3}$�ĸ���x1=3��x2=-$\frac{1}{3}$��
�۷���x-$\frac{1}{x}$=3+$\frac{3}{4}$�ĸ���x1=4��x2=-$\frac{1}{4}$��
�ܷ���x-$\frac{1}{x}$=4+$\frac{4}{5}$�ĸ���x1=5��x2=-$\frac{1}{5}$��
�ٹ۲��������̼���������������뷽��x-$\frac{1}{x}$=8$\frac{8}{9}$�ĸ���ʲô������֤��IJ��룮
���� �ѷ��̵ĸ��ֱ���뷽�̼�����֤��
���ݴ������ķ�ĸд�����̵ĸ���Ȼ����ʽ������֤���ɣ�
��� �⣺��x1=2ʱ�����=2-$\frac{1}{2}$�����=�ұߣ�
x2=-$\frac{1}{2}$ʱ�����=-$\frac{1}{2}$-$\frac{1}{-\frac{1}{2}}$=2-$\frac{1}{2}$�����=�ұߣ�
��x1=3ʱ�����=3-$\frac{1}{3}$�����=�ұߣ�
x2=-$\frac{1}{3}$ʱ�����=-$\frac{1}{3}$-$\frac{1}{-\frac{1}{3}}$=3-$\frac{1}{3}$�����=�ұߣ�
��x1=4ʱ�����=4-$\frac{1}{4}$=3+$\frac{3}{4}$�����=�ұߣ�
x2=-$\frac{1}{4}$ʱ�����=-$\frac{1}{4}$-$\frac{1}{-\frac{1}{4}}$=4-$\frac{1}{4}$=3+$\frac{3}{4}$�����=�ұߣ�
��x1=5ʱ�����=5-$\frac{1}{5}$=4+$\frac{4}{5}$�����=�ұߣ�
x2=-$\frac{1}{5}$ʱ�����=-$\frac{1}{5}$-$\frac{1}{-\frac{1}{5}}$=5-$\frac{1}{5}$=4+$\frac{4}{5}$�����=�ұߣ�
���룺����x-$\frac{1}{x}$=8$\frac{8}{9}$�ĸ���x1=9��x2=-$\frac{1}{9}$��
��֤���������߶�����9x�ã�9x2-9-80x=0��
��x-9����9x+1��=0��
x-9=0��9x+1=0��
���ԣ�x1=9��x2=-$\frac{1}{9}$��
���� ���⿼���˷�ʽ���̵Ľ⣬������Ŀ��Ϣ���۲�����̵Ľ���������ķ�ĸ�Ĺ�ϵ�ǽ���Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | 4cm | B�� | 5cm | C�� | 8cm | D�� | 9cm |
| A�� | x1=a��x2=$\frac{2}{a-1}$ | B�� | x1=a-1��x2=$\frac{2}{a-1}$ | C�� | x1=a��x2=$\frac{a+1}{a-1}$ | D�� | x1=a��x2=$\frac{a}{a-1}$ |
| A�� | 3 5 6 | B�� | 2 3 4 | C�� | 6 7 9 | D�� | 1.5 2 2.5 |
 ��ͼ��Rt��ABO�У���AOB=90�㣬��A�ڵ�һ���ޡ���B�ڵ������ޣ���AO��BO=1��$\sqrt{2}$������֪��A��˫����y=$\frac{1}{x}$�ϣ���B��˫����y=$\frac{k}{x}$�ϣ���k��ֵ��
��ͼ��Rt��ABO�У���AOB=90�㣬��A�ڵ�һ���ޡ���B�ڵ������ޣ���AO��BO=1��$\sqrt{2}$������֪��A��˫����y=$\frac{1}{x}$�ϣ���B��˫����y=$\frac{k}{x}$�ϣ���k��ֵ��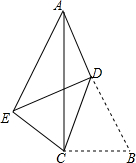 ��ͼ���ڡ�ABC�У���ACB=90�㣬BC=4��AB=10����D��AB�ϵ�һ�㣬����DBC����CD�۵�����ʱ��B���E�غϣ�����AE����DΪAB���е�ʱ��AE=$\frac{34}{5}$��
��ͼ���ڡ�ABC�У���ACB=90�㣬BC=4��AB=10����D��AB�ϵ�һ�㣬����DBC����CD�۵�����ʱ��B���E�غϣ�����AE����DΪAB���е�ʱ��AE=$\frac{34}{5}$��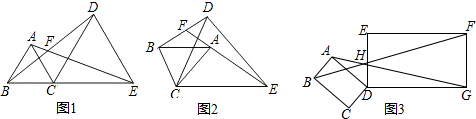
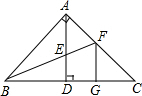 ��ͼ���ڡ�ABC�У���BAC=90�㣬AB=AC��AD��BC��BFƽ�֡�ABC����AD��E��FG��AD��
��ͼ���ڡ�ABC�У���BAC=90�㣬AB=AC��AD��BC��BFƽ�֡�ABC����AD��E��FG��AD��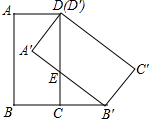 ��ͼ���ھ���ABCD�У�BC=1��������ABCD�Ƶ�D��ʱ����ת45�㣬�õ�����A��B��C��D�䣬��B��ǡ������BC���ӳ����ϣ���A��B�佻��CD�ڵ�E��
��ͼ���ھ���ABCD�У�BC=1��������ABCD�Ƶ�D��ʱ����ת45�㣬�õ�����A��B��C��D�䣬��B��ǡ������BC���ӳ����ϣ���A��B�佻��CD�ڵ�E��