Question

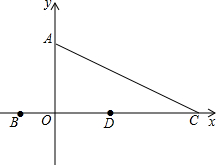如图，B、C两点的横坐标分别是一元二次方程-

1

4

x²+

3

2

x+4=0的两个跟，且A（0，4），点D是BC的中点，连接AC．
（1）点B的坐标为

 

，点C的坐标为

 

；
（2）求直线AC的解析式；
（3）线段AC上是否存在点E，使得△EDC为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由．

Answer 1

考点：一次函数综合题

专题：

分析：（1）求出方程的解即可；
（2）设直线AC的解析式是y=kx+b，把A、C的坐标代入即可求出答案；
（3）分为三种情况：①CE=CD，②CD=CE，③DE=CE，画出图形，结合图形证相似，得出比例式，即可求出答案．

解答：解：（1）解方程-

1

4

x²+

3

2

x+4=0得：x₁=-2，x₂=8，
即B的坐标是（-2，0），C的坐标是（8，0），
故答案为：（-2，0），（8，0）；

（2）设直线AC的解析式是y=kx+b，
把A、C的坐标代入得：

4=b 0=8k+b

，
解得：k=-

1

2

，b=4，
即直线AC的解析式是y=-

1

2

x+4；

（3）
线段AC上存在点E，使得△EDC为等腰三角形，
理由是：∵B（-2，0），C（8，0），
∴BC=10，
∵D为BC中点，
∴BD=DC=5，OD=8-5=3，
在Rt△AOD中，由勾股定理得：AD=5，
在Rt△AOC中，由勾股定理得：AC=

42+82

=4

5

，

①当E和A重合时，DE=DC=5，△EDC为等腰三角形，此时E的坐标是（0，4）；
②以C为圆心，以CD为半径作弧交线段AC于E₂，此时CD=CE₂，△EDC为等腰三角形，
过E₂作E₂M⊥BC于M，
∵∠CME₂=∠COA=90°，∠ACO=∠ACO，
∴△CME₂∽△COA，
∴

CE2

CA

=

ME2

OA

=

CM

OC

，
∴

5

4 5

=

ME2

4

=

CM

8

，
∴ME₂=

5

，CM=2

5

，
∴OM=8-2

5

，
即此时E的坐标是（8-2

5

，

5

）；
③作线段CD的垂直平分线交线段AC于E₃，则此时DE₃=CE₃，△EDC为等腰三角形，
CN=

1

2

CD=2.5，ON=8-2.5=5.5，
∵△AOC∽△E₃NC，
∴

NE3

AO

=

CN

OC

，
∴

NE3

4

=

2.5

8

，
∴NE₃=1.25，
即此时E的坐标是（5.5，1.25）．

点评：本题考查了用待定系数法求一次函数的解析式，相似三角形的性质和判定，等腰三角形的判定，解一元二次方程的应用，题目综合性比较强，有一定的难度．