题目内容
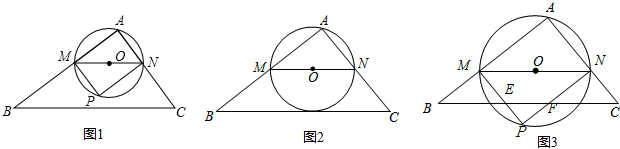
 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.(1)求线段DE的长;
(2)设直线ED分别交OA、OB的延长线于点M和点N,试问线段ME、ED、DN之间有什么数量关系,并说明理由;
(3)若BC=1,则△DOE的面积=
考点:圆的综合题,全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的判定与性质,勾股定理,三角形中位线定理,垂径定理,锐角三角函数的定义
专题:综合题
分析:(1)连接AB,如图1,由垂径定理可得D、E分别为BC、AC的中点,然后根据三角形中位线定理可得DE∥AB,ED=
AB,只需利用勾股定理求出AB的长,就可求出DE的长.
(2)连接OC并延长到点G,使得OG=OM,连接AB,如图2.由DE∥AB可证到∠M=∠N=45°,从而有OG=OM=ON.由OE垂直平分AC可以证到∠AOE=∠COE,从而可以证到△OEM≌△OEG,就可得到ME=GE,∠M=∠EGO;同理可得:DN=DG,∠N=∠DGO.就可证到∠EGD=90°.根据勾股定理可得DE2=EG2+DG2,则有DE2=ME2+DN2.
(3)过点D作DH⊥OE于H,连接OC,如图3,易得∠DOE=45°,OD=
.在Rt△OHD中可求出DH、OH的长,在Rt△DHE中可求出HE的长,就可求出△DOE的面积.
| 1 |
| 2 |
(2)连接OC并延长到点G,使得OG=OM,连接AB,如图2.由DE∥AB可证到∠M=∠N=45°,从而有OG=OM=ON.由OE垂直平分AC可以证到∠AOE=∠COE,从而可以证到△OEM≌△OEG,就可得到ME=GE,∠M=∠EGO;同理可得:DN=DG,∠N=∠DGO.就可证到∠EGD=90°.根据勾股定理可得DE2=EG2+DG2,则有DE2=ME2+DN2.
(3)过点D作DH⊥OE于H,连接OC,如图3,易得∠DOE=45°,OD=
| ||
| 2 |
解答:解:(1)连接AB,如图1.
∵OA=OB=2,∠AOB=90°,
∴∠OAB=∠OBA=45°,AB=
=2
.
∵OD⊥BC,OE⊥AC,
∴BD=DC,AE=EC.
∴DE为△ABC的中位线.
∴DE∥AB,DE=
AB=
.
∴线段DE的长为
.
(2)ED2=ME2+DN2.
证明:连接OC并延长到点G,使得OG=OM,连接AB,如图2.
∵DE∥AB(已证),
∴∠M=∠OAB=45°,∠N=∠OBA=45°.
∴∠M=∠N=45°.
∴OM=ON.
∴OM=ON=OG.
∵OE垂直平分AC,
∴OA=OC.
∴∠AOE=∠COE.
同理可得:∠COD=∠BOD.
在△OEM与△OEG中,
.
∴△OEM≌△OEG.
∴ME=GE,∠M=∠EGO.
同理可得:DN=DG,∠N=∠DGO.
∴∠EGD=∠EG0+∠DGO=∠M+∠N=45°+45°=90°.
∴DE2=EG2+DG2.
∴DE2=ME2+DN2.
(3)过点D作DH⊥OE于H,连接OC,如图3,
则有∠AOE=∠COE,∠COD=∠BOD(已证).
∴∠DOE=∠COD+∠COE
=
(∠COD+∠BOD+∠AOE+∠COE)
=
∠AOB=45°.
∵∠ODB=90°,OB=2,BD=
BC=
,
∴OD=
=
.
在Rt△OHD中,
DH=OD•sin∠DOH=
×
=
,
OH=OD•cos∠DOH=
×
=
.
在Rt△DHE中,
HE=
=
=
.
∴S△DOE=
OE•DH
=
×(
+
)×
=
.
故答案为:
.

∵OA=OB=2,∠AOB=90°,
∴∠OAB=∠OBA=45°,AB=
| OA2+OB2 |
| 2 |
∵OD⊥BC,OE⊥AC,
∴BD=DC,AE=EC.
∴DE为△ABC的中位线.
∴DE∥AB,DE=
| 1 |
| 2 |
| 2 |
∴线段DE的长为
| 2 |
(2)ED2=ME2+DN2.
证明:连接OC并延长到点G,使得OG=OM,连接AB,如图2.

∵DE∥AB(已证),
∴∠M=∠OAB=45°,∠N=∠OBA=45°.
∴∠M=∠N=45°.
∴OM=ON.
∴OM=ON=OG.
∵OE垂直平分AC,
∴OA=OC.
∴∠AOE=∠COE.
同理可得:∠COD=∠BOD.
在△OEM与△OEG中,
|
∴△OEM≌△OEG.
∴ME=GE,∠M=∠EGO.
同理可得:DN=DG,∠N=∠DGO.
∴∠EGD=∠EG0+∠DGO=∠M+∠N=45°+45°=90°.
∴DE2=EG2+DG2.
∴DE2=ME2+DN2.
(3)过点D作DH⊥OE于H,连接OC,如图3,
则有∠AOE=∠COE,∠COD=∠BOD(已证).
∴∠DOE=∠COD+∠COE
=
| 1 |
| 2 |
=
| 1 |
| 2 |
∵∠ODB=90°,OB=2,BD=
| 1 |
| 2 |
| 1 |
| 2 |

∴OD=
| OB2-BD2 |
| ||
| 2 |
在Rt△OHD中,
DH=OD•sin∠DOH=
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
OH=OD•cos∠DOH=
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
在Rt△DHE中,
HE=
| DE2-DH2 |
(
|
| ||
| 4 |
∴S△DOE=
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
=
15+
| ||
| 32 |
故答案为:
15+
| ||
| 32 |
点评:本题考查了垂径定理、三角形中位线定理、三角形全等的判定与性质、等腰三角形的判定与性质、垂直平分线的性质、三角函数、勾股定理、平行线的性质等知识,有一定的综合性,而通过构造全等三角形,将ME、ED、DN三条线段归结到同一个三角形中是解决第(2)小题的关键.

练习册系列答案
相关题目
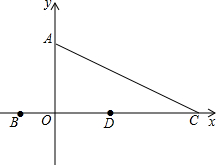 如图,B、C两点的横坐标分别是一元二次方程-
如图,B、C两点的横坐标分别是一元二次方程- 已知EC⊥AD于C,在EC取一点B,使BC=CD,连AB并延长交DE于F,AC=CE.
已知EC⊥AD于C,在EC取一点B,使BC=CD,连AB并延长交DE于F,AC=CE. 已知AB=AC,AD=AE,AB⊥AC,AD⊥AE.求证:
已知AB=AC,AD=AE,AB⊥AC,AD⊥AE.求证: