题目内容
 如图,已知在△ABC中AB的垂直平分线DM交BC于点D,点E为CD中点,∠CAE=25°,∠ACB=65°,求证:BD=AC.
如图,已知在△ABC中AB的垂直平分线DM交BC于点D,点E为CD中点,∠CAE=25°,∠ACB=65°,求证:BD=AC.考点:线段垂直平分线的性质
专题:证明题
分析:求出AE⊥DC,根据线段垂直平分线性质得出AD=AC,BD=AD,即可得出答案.
解答:
证明:连接AD,
∵∠CAE=25°,∠ACB=65°,
∴∠AED=∠CAE+∠ACB=90°,
即AE⊥DC,
∵点E为CD中点,
∴AD=AC,
∵AB的垂直平分线DM,
∴BD=AD,
∴BD=AC.

证明:连接AD,
∵∠CAE=25°,∠ACB=65°,
∴∠AED=∠CAE+∠ACB=90°,
即AE⊥DC,
∵点E为CD中点,
∴AD=AC,
∵AB的垂直平分线DM,
∴BD=AD,
∴BD=AC.
点评:本题考查了三角形外角性质,线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
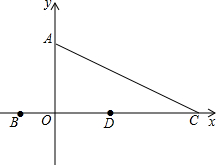 如图,B、C两点的横坐标分别是一元二次方程-
如图,B、C两点的横坐标分别是一元二次方程- 如图所示,OE平分∠AOC,OF平分∠BOC,若∠AOB+∠EOF=156°,求∠EOF的度数.
如图所示,OE平分∠AOC,OF平分∠BOC,若∠AOB+∠EOF=156°,求∠EOF的度数. 如图,直线y=kx+b,与抛物线y=ax2交于A(1,m),B(-2,4),与y轴交于点C
如图,直线y=kx+b,与抛物线y=ax2交于A(1,m),B(-2,4),与y轴交于点C