题目内容
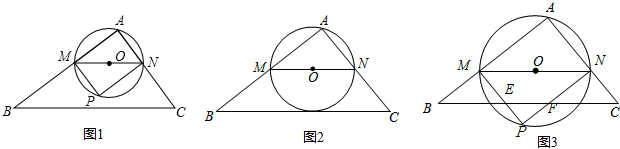
 如图,正方形ABCD的边长是8cm,以正方形的中心O为圆心,EF为直径的半圆切AB于M、切BC于N,已知C为BG的中点,AG交CD于H.P,Q同时从A出发,P以1cm/s的速度沿折线ADCG运动,Q以
如图,正方形ABCD的边长是8cm,以正方形的中心O为圆心,EF为直径的半圆切AB于M、切BC于N,已知C为BG的中点,AG交CD于H.P,Q同时从A出发,P以1cm/s的速度沿折线ADCG运动,Q以
| ||
| 2 |
(1)当t=4时,求证:△PEF≌△MEF;
(2)当0≤t≤8时,试判断PQ与CD的位置关系;
(3)当t>8时,是否存在t使得
| PQ | ||
EF2+16
|
| ||
| 16 |
考点:圆的综合题,二次函数的性质,二次函数的最值,平行线的判定,全等三角形的判定与性质,勾股定理,平行四边形的判定与性质,正方形的性质,切线的性质,相似三角形的判定与性质
专题:压轴题
分析:(1)连接OM,如图1,易证△AMO∽△ABC,从而得到AM=OM=4.当t=4时,AP=4=AM,从而可以证到△MAE≌△PAE,则有EM=EP,∠AEM=∠AEP,从而有∠MEF=∠PEF,就可证到△MEF≌△PEF.
(2)连接DG,如图2,由勾股定理可求出AG=8
.易证四边形ACGD是平行四边形,从而可求出DH=HC=4,AH=GH=4
.由AP=t,AQ=
t,AD=8,AH=4
可推出△PAQ∽△DAH,从而有∠AQP=∠AHD,则有PQ∥DC.
(3)过点Q作QT⊥DC于点T,如图3所示.由条件可得到8<t≤16.易证△HTQ∽△HCG,从而有HT=
-4,QT=t-8.进而可得到PT=
=
.根据勾股定理可得PQ2=
(t-
)2+
.利用二次函数的性质,由8<t≤16可得
≤PQ≤8.由EF=8得EF2+16
=64+16
.若
=
,可得PQ=4
+
,从而得到11<PQ<16.与“
≤PQ≤8”矛盾,故当t>8时,不存在t使得
=
.
(2)连接DG,如图2,由勾股定理可求出AG=8
| 5 |
| 5 |
| ||
| 2 |
| 5 |
(3)过点Q作QT⊥DC于点T,如图3所示.由条件可得到8<t≤16.易证△HTQ∽△HCG,从而有HT=
| t |
| 2 |
|
|
| 5 |
| 4 |
| 48 |
| 5 |
| 64 |
| 5 |
8
| ||
| 5 |
| 2 |
| 2 |
| PQ | ||
EF2+16
|
| ||
| 16 |
| 5 |
| 10 |
8
| ||
| 5 |
| PQ | ||
EF2+16
|
| ||
| 16 |
解答:解:(1)证明:连接OM,如图1,
当t=4时,AP=1×4=4.
∵EF为直径的半圆切AB于M,
∴OM⊥AB,即∠AMO=90°.
∵四边形ABCD是正方形,
∴∠ABC=90°,∠BAC=∠DAC=45°,AO=
AC.
∴∠AMO=∠ABC.
∴OM∥BC.
∴△AMO∽△ABC.
∴
=
=
.
∴AM=
AB=4,OM=
BC=4.
∴AM=AP.
在△MAE和△PAE中,
.
∴△MAE≌△PAE.
∴EM=EP,∠AEM=∠AEP.
∴∠MEF=∠PEF.
在△MEF和△PEF中,
.
∴△MEF≌△PEF.
(2)当0≤t≤8时,PQ∥CD.
证明:∵AP=t≤8,
∴点P在线段AD上,如图2.
连接DG,
∵AB=8,BG=16,∠ABG=90°,
∴AG=
=8
.
∵四边形ABCD是正方形,C为BG的中点,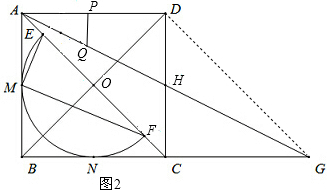
∴AD∥BC,AD=BC=CG.
∴AD∥CG,AD=CG.
∴四边形ACGD是平行四边形.
∴DH=HC=
DC=4,AH=GH=
AG=4
.
∵AP=t,AQ=
t,AD=8,AH=4
,
∴
=
=
.
∵∠PAQ=∠DAH,
∴△PAQ∽△DAH.
∴∠AQP=∠AHD.
∴PQ∥DC.
(3)当t>8时,不存在t使得
=
.
理由如下:
∵点P到达终点所用时间为
=24秒,点Q到达终点所用时间为
=16秒,
∴8<t≤16.
此时点P在DC上,点Q在HG上.
过点Q作QT⊥DC于点T,如图3所示.
∴∠HTQ=90°=∠HCG.
∴QT∥CG.
∴△HTQ∽△HCG.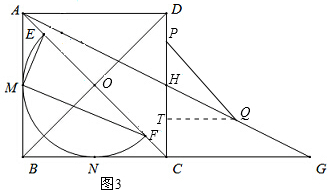
∴
=
=
.
∵HC=4,CG=8,HG=4
,HQ=
t-4
,
∴HT=
-4,QT=t-8.
∴DT=DH+HT=4+
-4=
.
∵DP=t-8,
∴PT=
=
.
∴PQ2=PT2+QT2=(8-
)2+(t-8)2
=
t2-24t+128
=
(t-
)2+
.
∵8<t≤16,
∴当t=
时,PQ2取最小值,最小值为
.
此时PQ=
.
当t=8时,PQ2=16,则PQ=4;
当t=16时,PQ2=64,则PQ=8.
∴
≤PQ≤8.
∵EF=20M=8,
∴EF2+16
=64+16
.
若
=
,
则PQ=
×(64+16
)=4
+
.
∵2<
<3,∴8<4
<12.
∵3<
<4,
∴11<4
+
<16.
∴11<PQ<16.
与“
≤PQ≤8”矛盾,
所以当t>8时,不存在t使得
=
.
当t=4时,AP=1×4=4.
∵EF为直径的半圆切AB于M,
∴OM⊥AB,即∠AMO=90°.
∵四边形ABCD是正方形,
∴∠ABC=90°,∠BAC=∠DAC=45°,AO=
| 1 |
| 2 |
∴∠AMO=∠ABC.
∴OM∥BC.
∴△AMO∽△ABC.

∴
| AM |
| AB |
| OM |
| BC |
| AO |
| AC |
∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=AP.
在△MAE和△PAE中,
|
∴△MAE≌△PAE.
∴EM=EP,∠AEM=∠AEP.
∴∠MEF=∠PEF.
在△MEF和△PEF中,
|
∴△MEF≌△PEF.
(2)当0≤t≤8时,PQ∥CD.
证明:∵AP=t≤8,
∴点P在线段AD上,如图2.
连接DG,
∵AB=8,BG=16,∠ABG=90°,
∴AG=
| AB2+BG2 |
| 5 |
∵四边形ABCD是正方形,C为BG的中点,

∴AD∥BC,AD=BC=CG.
∴AD∥CG,AD=CG.
∴四边形ACGD是平行四边形.
∴DH=HC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
∵AP=t,AQ=
| ||
| 2 |
| 5 |
∴
| AP |
| AD |
| t |
| 8 |
| AQ |
| AH |
∵∠PAQ=∠DAH,
∴△PAQ∽△DAH.
∴∠AQP=∠AHD.
∴PQ∥DC.
(3)当t>8时,不存在t使得
| PQ | ||
EF2+16
|
| ||
| 16 |
理由如下:
∵点P到达终点所用时间为
| 24 |
| 1 |
8
| ||||
|
∴8<t≤16.
此时点P在DC上,点Q在HG上.
过点Q作QT⊥DC于点T,如图3所示.
∴∠HTQ=90°=∠HCG.
∴QT∥CG.
∴△HTQ∽△HCG.

∴
| HT |
| HC |
| QT |
| CG |
| HQ |
| HG |
∵HC=4,CG=8,HG=4
| 5 |
| ||
| 2 |
| 5 |
∴HT=
| t |
| 2 |
∴DT=DH+HT=4+
| t |
| 2 |
| t |
| 2 |
∵DP=t-8,
∴PT=
|
|
∴PQ2=PT2+QT2=(8-
| t |
| 2 |
=
| 5 |
| 4 |
=
| 5 |
| 4 |
| 48 |
| 5 |
| 64 |
| 5 |
∵8<t≤16,
∴当t=
| 48 |
| 5 |
| 64 |
| 5 |
此时PQ=
8
| ||
| 5 |
当t=8时,PQ2=16,则PQ=4;
当t=16时,PQ2=64,则PQ=8.
∴
8
| ||
| 5 |
∵EF=20M=8,
∴EF2+16
| 2 |
| 2 |
若
| PQ | ||
EF2+16
|
| ||
| 16 |
则PQ=
| ||
| 16 |
| 2 |
| 5 |
| 10 |
∵2<
| 5 |
| 5 |
∵3<
| 10 |
∴11<4
| 5 |
| 10 |
∴11<PQ<16.
与“
8
| ||
| 5 |
所以当t>8时,不存在t使得
| PQ | ||
EF2+16
|
| ||
| 16 |
点评:本题考查了切线的性质、正方形的性质、相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、二次函数的性质、二次函数的最值、平行线的判定、勾股定理等知识,综合性非常强,难度比较大,而根据t的范围利用二次函数的性质确定PQ的范围是解决第(3)小题的关键.

练习册系列答案
相关题目
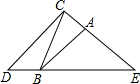 如图,∠E=40°,CD∥AB,∠ABE=2∠ABC,∠BCE=4∠ABC,
如图,∠E=40°,CD∥AB,∠ABE=2∠ABC,∠BCE=4∠ABC,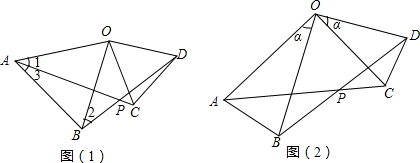
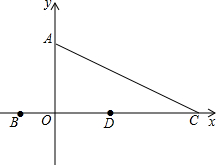 如图,B、C两点的横坐标分别是一元二次方程-
如图,B、C两点的横坐标分别是一元二次方程- 如图,直线y=kx+b,与抛物线y=ax2交于A(1,m),B(-2,4),与y轴交于点C
如图,直线y=kx+b,与抛物线y=ax2交于A(1,m),B(-2,4),与y轴交于点C 已知EC⊥AD于C,在EC取一点B,使BC=CD,连AB并延长交DE于F,AC=CE.
已知EC⊥AD于C,在EC取一点B,使BC=CD,连AB并延长交DE于F,AC=CE.