题目内容
10.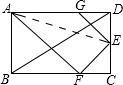 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处(AE为折痕,点E在CD上),在AD上截取DG,使以DG=CF.
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处(AE为折痕,点E在CD上),在AD上截取DG,使以DG=CF.(1)求证:△ABF∽△FCE;
(2)求证:BD⊥GE.
分析 (1)由四边形ABCD是矩形,可得∠ABF=∠C=∠ADC=90°,由折叠的性质可得:∠AFE=∠ADC=90°,然后由等角的余角相等,证得∠BAF=∠CFE,即可判定△ABF∽△FCE;
(2)由△ABF∽△FCE,DG=CF,易证得$\frac{DG}{DE}$=$\frac{AB}{AD}$,即可判定△DBA∽△EGD,继而可求得∠DGH+∠GDH=90°,则可得BD⊥GE.
解答 证明:(1)∵四边形ABCD是矩形,
∴∠ABF=∠C=∠ADC=90°,
∴∠BAF+∠BFA=90°,
由折叠的性质可得:∠AFE=∠ADC=90°,
∴∠CFE+∠BFA=90°,
∴∠BAF=∠CFE,
∴△ABF∽△FCE;
(2)∵DG=CF,DE=EF,
∴cos∠EFC=$\frac{FC}{EF}$=$\frac{DG}{DE}$,
∵cos∠BAF=$\frac{AB}{AF}$=$\frac{AB}{AD}$,∠BAF=∠EFC,
∴$\frac{DG}{DE}$=$\frac{AB}{AD}$,
∴$\frac{DG}{AB}$=$\frac{DE}{AD}$,
∵∠BAD=∠GDE=90°,
∴△DBA∽△EGD,
∴∠DBA=∠EGD,
∵∠DBA+∠ADB=90°,
∴∠DGH+∠GDH=90°,
∴∠GHD=90°,
∴BD⊥GE.
点评 此题考查了相似三角形的判定与性质、矩形的性质、折叠的性质以及三角函数等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.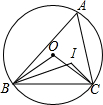 如图,△ABC的内心为I,∠A=52°,则∠BIC=116°,O为△ABC的外心,则∠BOC=100°.
如图,△ABC的内心为I,∠A=52°,则∠BIC=116°,O为△ABC的外心,则∠BOC=100°. 如图,点P是⊙O外一点,请用尺规过点P作⊙O的切线PA,切点为A(不写画法,保留作图痕迹).
如图,点P是⊙O外一点,请用尺规过点P作⊙O的切线PA,切点为A(不写画法,保留作图痕迹).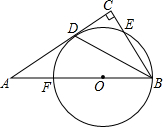 已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.
已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.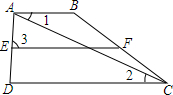 如图所示,已知AB∥EF,∠1=∠2,试说明∠3=∠D.
如图所示,已知AB∥EF,∠1=∠2,试说明∠3=∠D.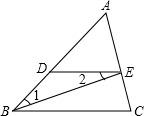 如图,BE平分∠ABC,且∠1=∠2,DE与BC平行吗?说明你的理由.
如图,BE平分∠ABC,且∠1=∠2,DE与BC平行吗?说明你的理由.