题目内容
6.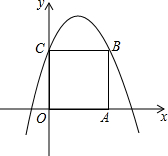 如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.
如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.
分析 根据正方形的性质得到B(2,2),C(0,2),然后把B点和C点坐标代入解析式得到关于a、b、c的方程组,再解方程组即可.
解答 解:∵正方形OABC的边长为2,
∴B(2,2),C(0,2),
把B(2,2),C(0,2)代入y=ax2+bx+c得$\left\{\begin{array}{l}{4a+2b+c=2}\\{c=2}\end{array}\right.$,
∴4a+2b=0,
∴2a=-b,
∴$\frac{a}{b}$=-$\frac{1}{2}$;
故答案为-$\frac{1}{2}$,
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
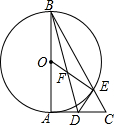 如图,△ABC中.△BAC=90°,以AB为直径作⊙O交BC于E,D为AC的中点,连结DE.
如图,△ABC中.△BAC=90°,以AB为直径作⊙O交BC于E,D为AC的中点,连结DE.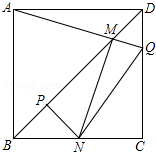 如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.
如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.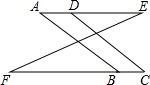 如图所示,已知AD∥BC,∠A=∠C,试说明∠ABF=∠C.
如图所示,已知AD∥BC,∠A=∠C,试说明∠ABF=∠C. 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.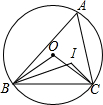 如图,△ABC的内心为I,∠A=52°,则∠BIC=116°,O为△ABC的外心,则∠BOC=100°.
如图,△ABC的内心为I,∠A=52°,则∠BIC=116°,O为△ABC的外心,则∠BOC=100°.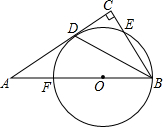 已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.
已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.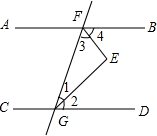 如图,∠1=∠2,∠3=∠4,且∠2+∠3=90°,试说明AB∥CD.
如图,∠1=∠2,∠3=∠4,且∠2+∠3=90°,试说明AB∥CD.