题目内容
5.如图,抛物线y=-x2+bx+c与x轴交于点A,B(1,0),与y轴交于点C(0,3).(1)求抛物线的解析式;
(2)如图①,点P在直线AC上,若S△PAO:S△PCO=2:1,求P点坐标;
(3)如图②,若点C关于对称轴对称的点为D,点E的坐标为(-2,0),F是OC的中点,连接DF,Q为线段AD上的一点,若∠EQF=∠ADF,求线段EQ的长.
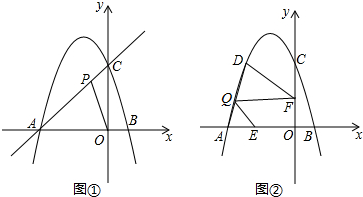
分析 (1)把B(1.0)、C(0,3)两点代入y=-x2+bx+c即可解决.
(2)如图①中,作PM⊥AB垂直为M,由PM∥CO,得$\frac{PA}{PC}$=$\frac{AM}{MO}$=$\frac{2}{1}$求出AM,即可解决问题.
(3)如图②中,连接CD,延长DF交x轴于H,先证明HD=HA,再证明△QAE∽△FDQ,得$\frac{QA}{DF}$=$\frac{AE}{DQ}$,设AQ=m,则DQ=AD-AQ=$\sqrt{10}$-m,列出方程即可解决.
解答 解:(1)把B(1.0)、C(0,3)两点代入y=-x2+bx+c得$\left\{\begin{array}{l}{c=3}\\{-1+b+c=0}\end{array}\right.$解得$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,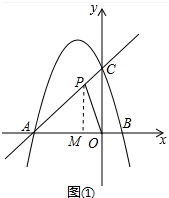
所以抛物线解析式为y=-x2-2x+3.
(2)如图①中,作PM⊥AB垂直为M,
令y=0,则-x2-2x+3=0,解得x=-3或1,
∴点A(-3,0),点B(1,0),点C(0,3),
设直线AC为y=kx+b,把A、C两点坐标代入得$\left\{\begin{array}{l}{b=3}\\{-3k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴直线AC为y=x+3,设点P(m,m+3),
∵若S△PAO:S△PCO=2:1,
∴PA:Pc=2:1,
∵PM∥CO,
∴$\frac{PA}{PC}$=$\frac{AM}{MO}$=$\frac{2}{1}$,
∴AM=2,MO=1,
∴m=-1,
∴点P坐标为(-1,2).
(3)如图②中,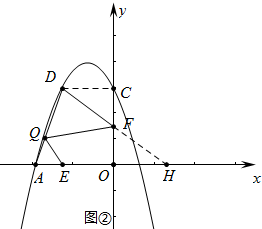 连接CD,延长DF交x轴于H.
连接CD,延长DF交x轴于H.
∵DC∥OH,
∴∠CDF=∠OHF,
在△CDF和△OHF中,
$\left\{\begin{array}{l}{∠CDF=∠OHF}\\{∠DFC=∠OFH}\\{FC=OF}\end{array}\right.$,
∴△CDF≌△OHF,
∴DC=OH,
∵点C(0,3),点D(-2,3),
∴点H(2,0),DH=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵AH=5,
∴HD=HA,
∴∠HDA=∠HAD,
∵∠AQF=∠ADF+∠DFQ=∠AQE+∠EQF,∠EQF=∠ADF,
∴∠AQE=∠DFQ,∵∠QAE=∠QDF,
∴△QAE∽△FDQ,
∴$\frac{QA}{DF}$=$\frac{AE}{DQ}$,设AQ=m,则DQ=AD-AQ=$\sqrt{10}$-m,
∴$\frac{1}{\sqrt{10}-m}$=$\frac{m}{\frac{5}{2}}$,
∴m=$\frac{\sqrt{10}}{2}$.
∵AD=$\sqrt{10}$,AQ=$\frac{\sqrt{10}}{2}$,
∴AQ=QD,
∴点Q坐标(-$\frac{5}{2}$,$\frac{3}{2}$),∵点E(-2,0),
∴QE=$\sqrt{(-\frac{5}{2}+2)^{2}+(\frac{3}{2})^{2}}$=$\frac{\sqrt{10}}{2}$.
点评 本题考查二次函数、一次函数、全等三角形的判定和性质、相似三角形的判定和性质勾股定理等知识,解题的关键是添加辅助线构造全等三角形,利用相似三角形的性质解决问题,学会把问题转化为方程,属于中考压轴题.

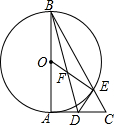 如图,△ABC中.△BAC=90°,以AB为直径作⊙O交BC于E,D为AC的中点,连结DE.
如图,△ABC中.△BAC=90°,以AB为直径作⊙O交BC于E,D为AC的中点,连结DE.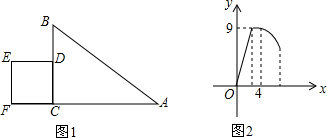
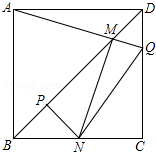 如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.
如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.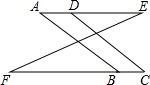 如图所示,已知AD∥BC,∠A=∠C,试说明∠ABF=∠C.
如图所示,已知AD∥BC,∠A=∠C,试说明∠ABF=∠C.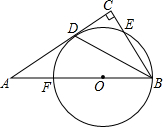 已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.
已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.