题目内容
15.不等式组$\left\{\begin{array}{l}{x+2>1}\\{3(1-x)-1≥-4}\end{array}\right.$的最小整数解为( )| A. | x=0 | B. | x=-1 | C. | x=1 | D. | x=2 |
分析 求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,即可求出最小整数解.
解答 解:$\left\{\begin{array}{l}{x+2>1①}\\{3(1-x)-1≥-4②}\end{array}\right.$,
由①得:x>-1,
由②得:x≤2,
所以不等式组的解集为-1<x≤2,
则不等式组最小的整数解为x=0,
故选A.
点评 本题考查了解一元一次不等式组,不等式组的整数解的应用,能求出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
6.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )
| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
3. 如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
 如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )| A. | 60° | B. | 25° | C. | 35° | D. | 45° |
10.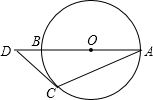 如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=( )
如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=( )
 如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=( )
如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=( )| A. | 40° | B. | 50° | C. | 55° | D. | 60° |
20.举反例说明“一个锐角的余角小于这个角”是假命题,下面错误的是( )
| A. | 设一个角是45°,它的余角是45°,但45°=45° | |
| B. | 设一个角是60°,它的余角是30°,但30°<60° | |
| C. | 设一个角是30°,它的余角是60°,但60°>30° | |
| D. | 设一个角是10°,它的余角是80°,但80°>10° |
7.当k<0,x>0时,反比例函数y=$\frac{k}{x}$的图象在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |

 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,那么当点R应运动到MQ中点时,△MNR的面积( )
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,那么当点R应运动到MQ中点时,△MNR的面积( ) 在如图所示的二次函数y=ax2+bx+c的图象中,大伟同学观察后得出了以下四条结论:①a<0,b>0,c>0;②b2-4ac=0;③$\frac{4ac-{b}^{2}}{4a}$<c;④关于x的一元二次方程ax2+bx+c=0有一个正根,你认为其中正确的结论有( )
在如图所示的二次函数y=ax2+bx+c的图象中,大伟同学观察后得出了以下四条结论:①a<0,b>0,c>0;②b2-4ac=0;③$\frac{4ac-{b}^{2}}{4a}$<c;④关于x的一元二次方程ax2+bx+c=0有一个正根,你认为其中正确的结论有( )