题目内容
10．
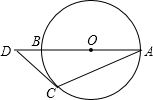如图，AB是⊙O的直径，点D在AB的延长线上，过点D作⊙O的切线，切点为C，若∠A=25°，则∠D=（ ）| A． | 40° | B． | 50° | C． | 55° | D． | 60° |
分析 连接OC，先根据圆周角定理得∠DOC=2∠A=50°，再根据切线的性质定理得∠OCD=90°，则此题易解．
解答 
解：连接OC，
∵OA=OC，
∴∠A=∠OCA=25°，
∴∠DOC=2∠A=50°，
∵过点D作⊙O的切线，切点为C，
∴∠OCD=90°，
∴∠D=40°．
故选：A．
点评 此题综合运用了切线的性质定理、圆周角定理和直角三角形的两个锐角互余的性质，熟记和圆的切线有关的各种性质是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
20．计算（-0.25）2013×42013的结果是（ ）
| A． | -1 | B． | 1 | C． | 0.25 | D． | 44026 |
1．给出下列命题①三条线段组成的图形叫三角形，②三角形的三条高相交于三角形内同一点，③任何一个三角形都有三条角平分线、三条中线、三条高④三角形的内角和等于外角和、⑤多边形的内角和大于外角和⑥三角形的三条角平分线相交于形内同一点．其中正确的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
18．
如图，已知直线AB与CD相交于点O，若∠AOC+∠BOD=140°，则∠AOC的度数为（ ）
如图，已知直线AB与CD相交于点O，若∠AOC+∠BOD=140°，则∠AOC的度数为（ ）| A． | 40° | B． | 70° | C． | 110° | D． | 140° |
5．将二次函数y=x2-4x+3化为y=（x-h）2+k的形式，下列结果正确的是（ ）
| A． | y=（x+2）2+1 | B． | y=（x+2）2-1 | C． | y=（x-2）2-1 | D． | y=（x-2）2+1 |
15．不等式组$\left\{\begin{array}{l}{x+2＞1}\\{3（1-x）-1≥-4}\end{array}\right.$的最小整数解为（ ）
| A． | x=0 | B． | x=-1 | C． | x=1 | D． | x=2 |
2．用直尺和圆规操作一个角等于已知角的依据是（ ）
| A． | SAS | B． | SSS | C． | AAS | D． | ASA |
19．
如图，在?ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则AB的长为（ ）
如图，在?ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则AB的长为（ ）| A． | 4 | B． | 3 | C． | $\frac{5}{2}$ | D． | 2 |
20．纳米是一种长度单位，1纳米=10-9米，已知某种植物花粉的直径约为35000纳米，那么用科学记数法表示该种花粉的直径为（ ）
| A． | 3.5×104米 | B． | 3.5×10-4米 | C． | 3.5×10-5米 | D． | 3.5×10-9米 |