题目内容
15.已知一次函数y=kx+b的图象经过点(1,-2),(3,2).若该图象分别交x轴,y轴于A、B两点,O为坐标原点,求AOB的面积.分析 将两点坐标代入一次函数解析式求出k与b的值,再根据k与b的值确定出一次函数解析式,分别令x与y为0求出对应y与x的值,确定出AO与OB的长,即可求出三角形AOB面积.
解答 解:将(1,-2)与(3,2)代入y=kx+b得:
$\left\{\begin{array}{l}{k+b=-2}\\{3k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-4}\end{array}\right.$,
则一次函数解析式为y=2x-4;
令x=0,得到y=-4;令y=0,得到x=2,
故OA=4,OB=2,
则S△AOB=$\frac{1}{2}$OA•OB=4.
点评 此题考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
5.下列各数中,最小的数是( )
| A. | -3 | B. | -$\frac{1}{2}$ | C. | 2 | D. | 0 |
6.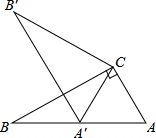 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )
 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )| A. | 150° | B. | 90° | C. | 60° | D. | 30° |
3.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{3}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{{a}^{2}b}$ |
20.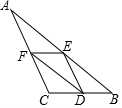 如图,△ABC的周长26cm,中位线EF=3cm,中位线DF=6cm,则中位线DE的长为( )
如图,△ABC的周长26cm,中位线EF=3cm,中位线DF=6cm,则中位线DE的长为( )
 如图,△ABC的周长26cm,中位线EF=3cm,中位线DF=6cm,则中位线DE的长为( )
如图,△ABC的周长26cm,中位线EF=3cm,中位线DF=6cm,则中位线DE的长为( )| A. | 4cm | B. | 4.5cm | C. | 5cm | D. | 8cm |
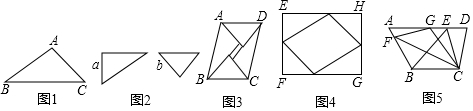
7.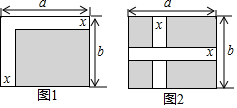 通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )
通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )
 通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )
通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )| A. | a(b-x)=ab-ax | B. | b(a-x)=ab-bx | ||
| C. | (a-x)(b-x)=ab-ax-bx | D. | (a-x)(b-x)=ab-ax-bx+x2 |
4.在下列所给的坐标的点中,在第二象限的是( )
| A. | (1,-2) | B. | (-1,-4) | C. | (-2,5) | D. | (0,1) |