题目内容
3.下列二次根式中,是最简二次根式的是( )| A. | $\sqrt{12}$ | B. | $\sqrt{3}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{{a}^{2}b}$ |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:A、$\sqrt{12}$=2$\sqrt{3}$,$\sqrt{12}$不是最简二次根式;
B、3不能再开方,$\sqrt{3}$是最简二次根式;
C、$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,$\sqrt{\frac{1}{2}}$不是最简二次根式;
D、$\sqrt{{a}^{2}b}$=|a|$\sqrt{b}$,$\sqrt{{a}^{2}b}$不是最简二次根式.
故选B.
点评 本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:
(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
14.下列方程组中是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=6}\\{x=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+z=0}\\{3x-y=\frac{1}{5}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\frac{1}{x}+y=5}\\{2x-5y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=3}\\{xy=1}\end{array}\right.$ |
18. 如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )
如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )
 如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )
如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )| A. | 55° | B. | 65° | C. | 25° | D. | 35° |
8.已知反比例函数y=$\frac{3}{x}$,在此函数图象上的点是( )
| A. | (-1,1) | B. | (1,1) | C. | (1,3) | D. | (-1,3) |
12.给出下列命题:
(1)三角形的一个外角一定大于它的一个内角
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形
(3)三角形的最小内角不能大于60°
(4)三角形的一个外角等于和它不相邻的两个内角的和
其中真命题的个数是( )
(1)三角形的一个外角一定大于它的一个内角
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形
(3)三角形的最小内角不能大于60°
(4)三角形的一个外角等于和它不相邻的两个内角的和
其中真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.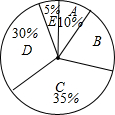 自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( )
自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( )
 自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( )
自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( ) | 组别 | 月用水量x(单位:吨) |
| A | 0≤x<3 |
| B | 3≤x<6 |
| C | 6≤x<9 |
| D | 9≤x<12 |
| E | x>12 |
| A. | 18户 | B. | 20户 | C. | 22户 | D. | 24户 |
 如图,在平面直角坐标系xOy中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,2),B(n,-1),其中m>0,n<0.
如图,在平面直角坐标系xOy中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,2),B(n,-1),其中m>0,n<0. 如图,在平面直角坐标系中,点A、B分别是x轴、y轴上的点,且OA=a,OB=b,其中a、b满足$\sqrt{a+b-32}$+|b-a+16|=0,将B向左平移18个单位得到点C.
如图,在平面直角坐标系中,点A、B分别是x轴、y轴上的点,且OA=a,OB=b,其中a、b满足$\sqrt{a+b-32}$+|b-a+16|=0,将B向左平移18个单位得到点C.