题目内容
6.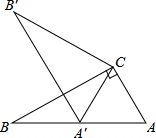 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,使得点A′恰好落在AB边上,则α等于( )| A. | 150° | B. | 90° | C. | 60° | D. | 30° |
分析 由在Rt△ABC中,∠ACB=90°,∠ABC=30°,可求得∠A的度数,又由将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,易得△ACA′是等边三角形,继而求得答案.
解答 解:∵在Rt△ABC中,∠ACB=90°,∠ABC=30°,
∴∠A=90°-∠ABC=60°,
∵将△ABC绕点C顺时针旋转α角(0°<α<180°)至△A′B′C′,
∴AC=A′C,
∴△ACA′是等边三角形,
∴α=∠ACA′=60°.
故选C.
点评 此题考查了旋转的性质以及等边三角形的判定与性质.注意证得△ACA′是等边三角形是关键.

练习册系列答案
相关题目
17.下列分式中,属于最简分式的是( )
| A. | $\frac{6}{3x}$ | B. | $\frac{4x}{{x}^{2}+3x}$ | C. | $\frac{x+2}{{x}^{2}+4}$ | D. | $\frac{3-x}{x-3}$ |
14.下列方程组中是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=6}\\{x=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+z=0}\\{3x-y=\frac{1}{5}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\frac{1}{x}+y=5}\\{2x-5y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=3}\\{xy=1}\end{array}\right.$ |
18. 如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )
如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )
 如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )
如图,已知AB∥CD,EF⊥CD,若∠1=125°,则∠2的度数为( )| A. | 55° | B. | 65° | C. | 25° | D. | 35° |
16.某花卉基地种植了郁金香和玫瑰两种花卉共30亩,有关数据如表:
(1)设种植郁金香x亩,两种花卉总收益为y万元,求y关于x的函数关系式.(收益=销售额-成本)
(2)若计划投入的成本的总额不超过70万元,要使获得的收益最大,基地应种植郁金香和玫瑰个多少亩?
| 成本 (单位:万元/亩) | 销售额 (单位:万元/亩) | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
(2)若计划投入的成本的总额不超过70万元,要使获得的收益最大,基地应种植郁金香和玫瑰个多少亩?
 如图,在平面直角坐标系中,点A、B分别是x轴、y轴上的点,且OA=a,OB=b,其中a、b满足$\sqrt{a+b-32}$+|b-a+16|=0,将B向左平移18个单位得到点C.
如图,在平面直角坐标系中,点A、B分别是x轴、y轴上的点,且OA=a,OB=b,其中a、b满足$\sqrt{a+b-32}$+|b-a+16|=0,将B向左平移18个单位得到点C.