题目内容
16.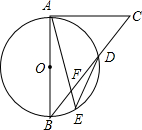 如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )
如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 连接AD,BE,根据圆的性质得到∠DBE=∠DEF,AD=DE,推出△BDE∽△EDF,根据相似三角形的性质得到DE2=BD•DF,求得$\frac{DE}{DF}$=$\sqrt{2}$,BE=$\sqrt{2}$EF,根据勾股定理得到AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=$\sqrt{3}$DF,根据相交弦定理得到AF•EF=BF•DF,求得EF=$\frac{\sqrt{3}}{3}$DF,根据圆周角定理得到∠BAE=∠BDE,根据三角函数的定义即可得到结论.
解答 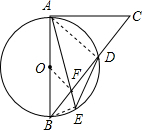 解:连接AD,BE,
解:连接AD,BE,
∵$\widehat{AD}$=$\widehat{DE}$,
∴∠DBE=∠DEF,AD=DE,
∵∠FDE=∠BDE,
∴△BDE∽△EDF,
∴$\frac{DE}{BD}=\frac{DF}{DE}$,
∴DE2=BD•DF,
∵DF=BF,
∴DE=AD=$\sqrt{2}$DF,
∴$\frac{DE}{DF}$=$\sqrt{2}$,
∵△BDE∽△EDF,
∴$\frac{BE}{EF}=\frac{DE}{DF}$=$\sqrt{2}$,
∴BE=$\sqrt{2}$EF,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=$\sqrt{3}$DF,
∵AE交BD于F,
∴AF•EF=BF•DF,
∴$\sqrt{3}$DF•EF=DF2,
∴EF=$\frac{\sqrt{3}}{3}$DF,
∴BE=$\frac{\sqrt{6}}{3}$DF,AE=AF+EF=$\frac{4\sqrt{3}}{3}$DF,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵∠BAE=∠BDE,
∴tan∠BDE=tan∠BAE=$\frac{BE}{AE}$═$\frac{\frac{\sqrt{6}}{3}DF}{\frac{4\sqrt{3}}{3}DF}$=$\frac{\sqrt{2}}{4}$.
故选B.
点评 本题考查了切线的性质,勾股定理,相似三角形的判定和性质,三角函数的定义,正确的作出辅助线是解题的关键.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
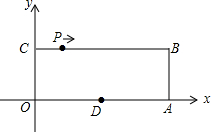 如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动. 已知二次函数y=x2+mx+n的图象经过点A(1,0)和D(4,3),与x轴的另一个交点为B,与y轴交于点C.
已知二次函数y=x2+mx+n的图象经过点A(1,0)和D(4,3),与x轴的另一个交点为B,与y轴交于点C.