题目内容
6．若分式-$\frac{{a}^{2}}{2a-6}$的值为正，则a的取值范围是a＜3且a≠0．分析 直接利用分式的符号得出2a-6＜0，进而求出答案．
解答 解：∵分式-$\frac{{a}^{2}}{2a-6}$的值为正，
∴2a-6＜0，a2≠0，
解得：a＜3，且a≠0．
故答案为：a＜3且a≠0．
点评 此题主要考查了分式的值，正确得出2a-6的符号是解题关键．
练习册系列答案
相关题目
16．下列调查中，最适宜采取普查的（ ）
| A． | 一批洗衣机的使用寿命 | |
| B． | 了解某市中学生课外阅读的情况 | |
| C． | 《新闻联播》电视栏目的收视率 | |
| D． | 调查乘坐飞机的旅客是否携带了危禁物品 |
17．
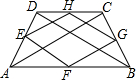如图，四边形ABCD中，AB∥DC，E，F，G，H分别是各边的中点，分别记四边形ABCD和EFGH的面积为S1和S2，则下列各个判断中正确的是（ ）
如图，四边形ABCD中，AB∥DC，E，F，G，H分别是各边的中点，分别记四边形ABCD和EFGH的面积为S1和S2，则下列各个判断中正确的是（ ）| A． | S1＞2S2 | B． | 2S1＜S2 | C． | S1=2S2 | D． | $\sqrt{{S}_{1}}$=2$\sqrt{{S}_{2}}$ |
14．
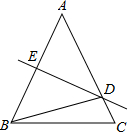如图，在△ABC中，AB=AC，AB的垂直平分线DE交AC于D，交AB于E，∠DBC=15°，则∠A的度数是（ ）
如图，在△ABC中，AB=AC，AB的垂直平分线DE交AC于D，交AB于E，∠DBC=15°，则∠A的度数是（ ）| A． | 50° | B． | 20° | C． | 30° | D． | 25° |
如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10cm，小圆半径为10cm，小圆半径为6cm，则弦AB的长为16cm．
15．
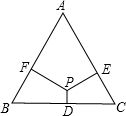如图，P为等腰三角形ABC内一点，过P分别作三条边BC、CA、AB的垂线，垂足分别为D、E、F．已知AB=AC=10，BC=12，且PD：PE：PF=1：3：3．则四边形PDCE的面积为（ ）
如图，P为等腰三角形ABC内一点，过P分别作三条边BC、CA、AB的垂线，垂足分别为D、E、F．已知AB=AC=10，BC=12，且PD：PE：PF=1：3：3．则四边形PDCE的面积为（ ）| A． | 10 | B． | 15 | C． | $\frac{40}{3}$ | D． | $\frac{50}{3}$ |
16．
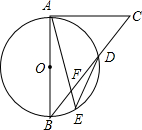如图，AB为⊙O的直径，CA为⊙O的切线，CB交⊙O于D，$\widehat{AD}$=$\widehat{DE}$，AE交BD于F，若DF=BF，则tan∠BDE的值为（ ）
如图，AB为⊙O的直径，CA为⊙O的切线，CB交⊙O于D，$\widehat{AD}$=$\widehat{DE}$，AE交BD于F，若DF=BF，则tan∠BDE的值为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |