15.(本小题满分14分)
已知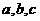 分别为
分别为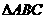 的角A、B、C的对应边,
的角A、B、C的对应边,
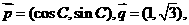 且
且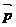 ∥
∥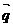 ,
,
(Ⅰ)求:角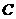 的大小;
的大小;
(Ⅱ)若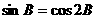 ,且
,且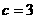 ,求
,求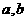 的值。
的值。
16.(本小题满分14分)
已知等比数列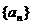 中,公比
中,公比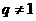 ,且
,且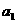 是
是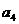 与
与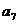 的等差中项,
的等差中项,
前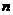 项和为
项和为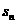 ,数列
,数列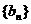 满足:
满足: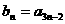

(Ⅰ)若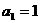 ,求数列
,求数列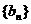 的前
的前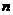 项的和
项的和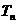 ;
;
(Ⅱ)若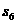 +
+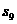 =
=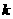
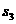 ,求
,求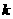 的值。
的值。
17.(本小题满分14分)
甲、乙两人进行两种游戏,两种游戏的规则由下表给出:
(球的大小都相同)
|
游戏1 |
游戏2 |
|
裁判的口袋中有4个白球和5个红球 |
甲的口袋中有6个白球和2个红球 乙的口袋中有3个白球和5个红球 |
|
由裁判摸两次,每次摸一个,记下颜色后放回 |
每人都从自己的口袋中摸一个球 |
|
摸出的两球同色→甲胜 摸出的两球不同色→乙胜 |
摸出的两球同色→甲胜 摸出的两球不同色→乙胜 |
(Ⅰ)分别求出在游戏1中甲、乙获胜的概率;
(Ⅱ)求出在游戏2中甲获胜的概率,并说明这两种游戏哪种游戏更公平。
18.(本小题满分14分)
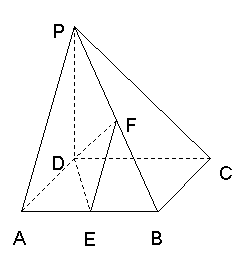
如图:在四棱锥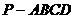 中,
中,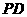 ⊥底面
⊥底面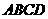 ,
,
底面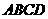 为正方形,
为正方形,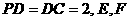 分别是
分别是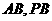 的中点,
的中点,
(Ⅰ)求证: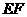 ⊥
⊥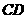 ;
;
(Ⅱ)求面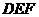 与面
与面 所成二面角的大小;(用反三角表示)
所成二面角的大小;(用反三角表示)
19.(本小题满分14分)
已知函数
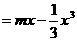 的定义域为
的定义域为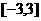 ,
,
(Ⅰ)当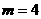 时,若函数
时,若函数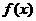 的导数
的导数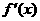 满足关系
满足关系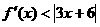 ,求
,求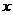 的取值范围;
的取值范围;
(Ⅱ)若函数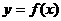 同时满足以下两个条件:①函数
同时满足以下两个条件:①函数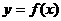 在
在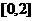 上单调递增;②函数
上单调递增;②函数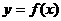 ,
,
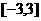 的图象的最高点落在直线
的图象的最高点落在直线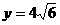 上,求
上,求 的值。
的值。
20.(本小题满分14分)
已知点A、F分别为双曲线C: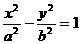
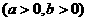
的右顶点、右焦点,点B的坐标为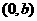 ,且
,且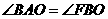 (其中O为坐标原点).
(其中O为坐标原点).
(Ⅰ)求双曲线C的离心率;
(Ⅱ)求证:三条直线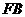 、双曲线C的渐近线
、双曲线C的渐近线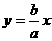 、右准线交于一点;
、右准线交于一点;
(Ⅲ)是否存在直线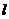 经过点F,与双曲线C的右支交于点P,与
经过点F,与双曲线C的右支交于点P,与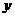 轴交于点Q,使点P恰是线段FQ的中点,若存在,求出直线
轴交于点Q,使点P恰是线段FQ的中点,若存在,求出直线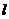 的斜率,若不存在,请说明理由。
的斜率,若不存在,请说明理由。
2006年温州市高三第二次适应性模拟测试
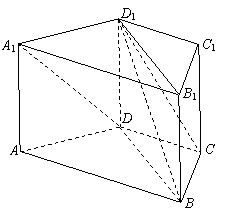 求:(1)AD与BD1所成的角;
求:(1)AD与BD1所成的角;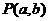 是由四条直线
是由四条直线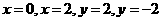 所围成的矩形区域(包括边界)内的动点,则动点
所围成的矩形区域(包括边界)内的动点,则动点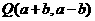 形成的平面区域的面积为 ▲ 。
形成的平面区域的面积为 ▲ 。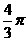 的球放在一个正三棱柱的盒子里,这个球面恰好与这正三棱柱的所有面都相切,则这正三棱柱的底面边长为 ▲ 。
的球放在一个正三棱柱的盒子里,这个球面恰好与这正三棱柱的所有面都相切,则这正三棱柱的底面边长为 ▲ 。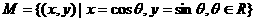 ,
,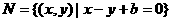
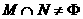 ,则
,则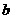 的取值范围是 ▲ 。
的取值范围是 ▲ 。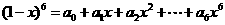 ,则
,则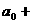
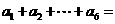 ▲
▲ 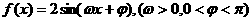 的最小正周期为
的最小正周期为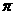 ,且为偶函数
,且为偶函数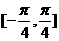 B.
B.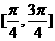 C.
C.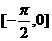 D.
D.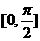
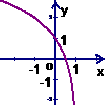
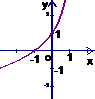
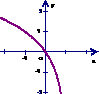
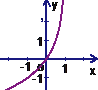
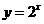 的反函数是
的反函数是 ,则函数
,则函数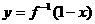 的图象是 ( )
的图象是 ( )