0 48124 48132 48138 48142 48148 48150 48154 48160 48162 48168 48174 48178 48180 48184 48190 48192 48198 48202 48204 48208 48210 48214 48216 48218 48219 48220 48222 48223 48224 48226 48228 48232 48234 48238 48240 48244 48250 48252 48258 48262 48264 48268 48274 48280 48282 48288 48292 48294 48300 48304 48310 48318 447348
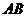 是
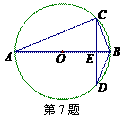
是 的直径,
的直径,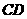 为弦,
为弦,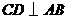 于
于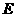 ,
,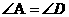 B.
B.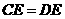
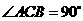 D.
D.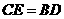
 A.方差 B.中位数
A.方差 B.中位数 
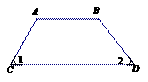
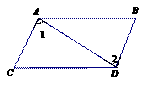
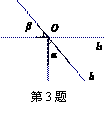
 下列图形中,由
下列图形中,由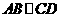 ,能得到
,能得到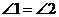 的是
的是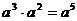 B.
B.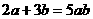 C.
C.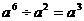 D.
D.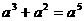
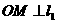 ,若
,若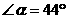 ,则
,则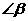 等于
等于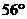 B.
B.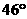
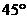 D.
D.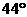
 A.
A.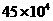 B.
B. 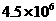 C.
C. 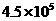 D.
D. 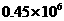
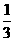 的相反数是
的相反数是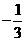
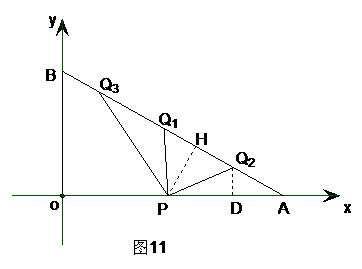
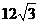 cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以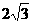 cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.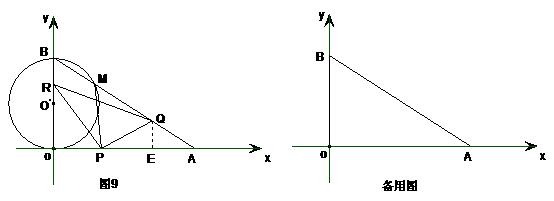 (4)是否存在△APQ为等腰三角形,若存在,求出相应的t值,若不存在请说明理由.
(4)是否存在△APQ为等腰三角形,若存在,求出相应的t值,若不存在请说明理由.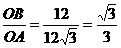
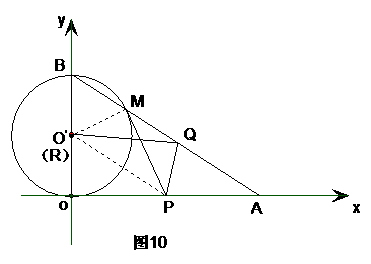 由(1)知∠OBA=60°
由(1)知∠OBA=60°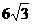
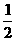 AQ=2t
AQ=2t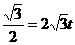
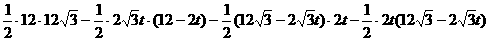
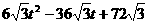
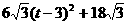 (
(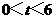 )
) 当t=3时,S△PQR最小=
当t=3时,S△PQR最小=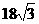
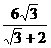
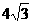 t
t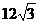 -
-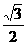 =18-3t
=18-3t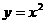 的图像如图8所示,请将此图像向右平移1个单位,再向下平移2个单位.
的图像如图8所示,请将此图像向右平移1个单位,再向下平移2个单位.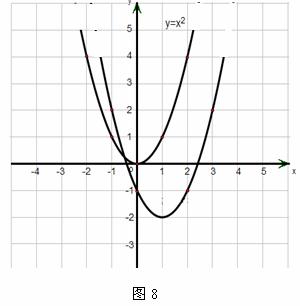 解:画图如图所示:
解:画图如图所示: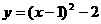
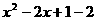
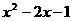
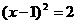
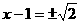
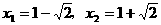
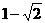 ,0)和(
,0)和(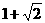 ,0)
,0)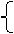 7x<28
7x<28