3.一家鞋店对上周某一品牌女鞋的销售量统计如下:
|
尺码/厘米 |
22 |
22.5 |
23 |
23.5 |
24 |
24.5 |
25 |
|
销售量/双 |
1 |
2 |
5 |
11 |
7 |
3 |
1 |
该鞋店决定本周进该品牌女鞋时多进一些尺码为23.5厘米的鞋,影响鞋店决策的统计量是
A.平均数 B.众数 C.中位数 D.方差
24.(满分10分)小王家是新农村建设中涌现出的“养殖专业户”.他准备购置80只相同规格的网箱,养殖A、B两种淡水鱼(两种鱼不能混养).计划用于养鱼的总投资不少于7万元,但不超过7.2万元,其中购置网箱等基础建设需要1.2万元.设他用x只网箱养殖A种淡水鱼,目前平均每只网箱养殖A、B两种淡水鱼所需投入及产业情况如下表:
|
|
鱼苗投资 (百元) |
饮料支出 (百元) |
收获成品鱼 (千克) |
成品鱼价格 (百元/千克) |
|
A种鱼 |
2.3 |
3 |
100 |
0.1 |
|
B种鱼 |
4 |
5.5 |
55 |
0.4 |
(1)小王有哪几种养殖方式?
(2)哪种养殖方案获得的利润最大?
(3)根据市场调查分析,当他的鱼上市时,两种鱼的价格会有所变化,A种鱼价格上涨a%(0<a<50),B种鱼价格下降20%,考虑市场变化,哪种方案获得的利润最大?(利润=收入-支出.收入指成品鱼收益,支出包括基础建设投入、鱼苗投资及饲料支出)
|
|
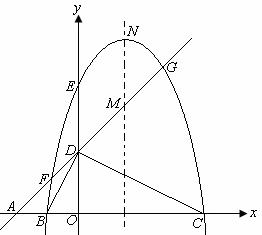
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
|
21.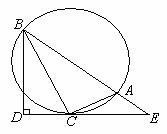 (8分)如图,Rt△BDE中,∠BDE=90°,BC平分∠DBE交DE于点C,AC⊥CB交BE于点A,△ABC的外接圆的半径为r.
(8分)如图,Rt△BDE中,∠BDE=90°,BC平分∠DBE交DE于点C,AC⊥CB交BE于点A,△ABC的外接圆的半径为r.
(1)求证: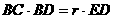 ;
;
(2)若BD=3,DE=4,求AE的长.
|
|
 交x轴于点A,交y轴于点B,将△AOB沿直线l翻折,点O的对应点C恰好落在双曲线
交x轴于点A,交y轴于点B,将△AOB沿直线l翻折,点O的对应点C恰好落在双曲线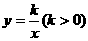 上.
上.
(1)求k的值;
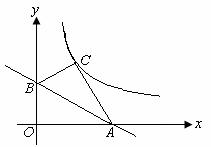 (2)将△ABC绕AC的中点旋转180°得到△PCA,请判断点P是否在双曲线
(2)将△ABC绕AC的中点旋转180°得到△PCA,请判断点P是否在双曲线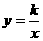 上,并说明理由.
上,并说明理由.
|
19.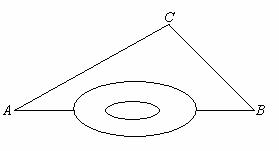 (满分7分)如图,A、B两地被一大山阻隔,汽车从A地到B须经过C地中转.为了促进A、B两地的经济发展,现计划开通隧道,使汽车可以直接从A地到B地.已知∠A=30°,∠B=45°,BC=
(满分7分)如图,A、B两地被一大山阻隔,汽车从A地到B须经过C地中转.为了促进A、B两地的经济发展,现计划开通隧道,使汽车可以直接从A地到B地.已知∠A=30°,∠B=45°,BC= 千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从A地到B地需要多长时间?(参考数据:
千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从A地到B地需要多长时间?(参考数据: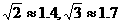 )
)
|
|
(1)写出表格中得分的众数,中位数和平均数;
(2)学校从获胜班级的代表队中各抽取1名学生组成“绿色环保监督”小组,小明、小红分别是七(4)班和七(6)班代表队的学生,用列表法或画树形图的方法说明同时抽到小明和小红的概率是多少?
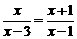 的解为
的解为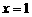 B.
B.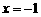 C.
C.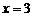 D.
D.
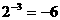 B.
B.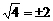 C.
C.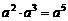 D.
D.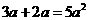
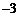 的绝对值是
的绝对值是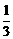 D.
D.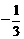
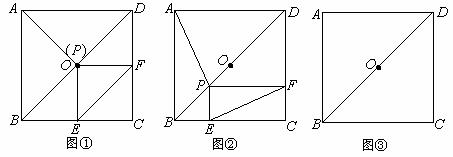
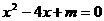 的一个根为-2,求方程的另一根及m的值.
的一个根为-2,求方程的另一根及m的值.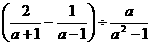 ,其中
,其中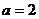 .
.