0 47767 47775 47781 47785 47791 47793 47797 47803 47805 47811 47817 47821 47823 47827 47833 47835 47841 47845 47847 47851 47853 47857 47859 47861 47862 47863 47865 47866 47867 47869 47871 47875 47877 47881 47883 47887 47893 47895 47901 47905 47907 47911 47917 47923 47925 47931 47935 47937 47943 47947 47953 47961 447348
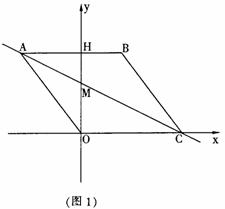
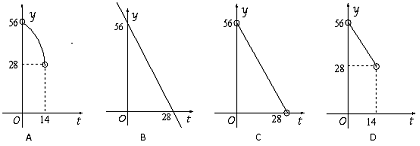 如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形AMND的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是(
)
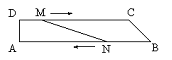
如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形AMND的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是(
)
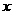 秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或在CB上时的坐标(用含
秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或在CB上时的坐标(用含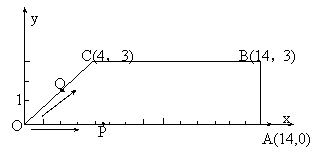 分析:本例是平面直角坐标系与方程、函数、不等式及几何型问题的综合题,解题关键是正确地用
分析:本例是平面直角坐标系与方程、函数、不等式及几何型问题的综合题,解题关键是正确地用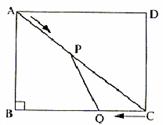
 ① 求S关于t的函数关系式;
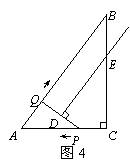
① 求S关于t的函数关系式;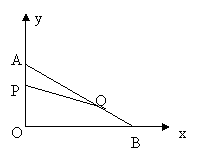 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ与△AOB相似? (3) 当t为何值时,△APQ的面积为
如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ与△AOB相似? (3) 当t为何值时,△APQ的面积为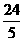 个平方单位?
个平方单位?
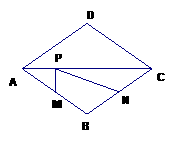
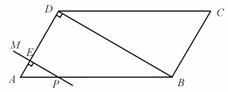
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是线段AC上的两个动点,分别从A、C两点以相同的速度1㎝/s向C、A运动,若BD=12㎝,AC=16㎝,当t
时,四边形DEBF为平行四边形;当时间t=
时,四边形DEBF为矩形。
如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是线段AC上的两个动点,分别从A、C两点以相同的速度1㎝/s向C、A运动,若BD=12㎝,AC=16㎝,当t
时,四边形DEBF为平行四边形;当时间t=
时,四边形DEBF为矩形。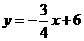 与坐标轴分别交于
与坐标轴分别交于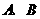 两点,动点
两点,动点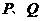 同时从
同时从 点出发,同时到达
点出发,同时到达 点,运动停止.点
点,运动停止.点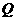 沿线段
沿线段 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点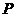 沿路线
沿路线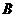 →
→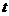 秒,
秒, 的面积为
的面积为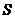 ,求出
,求出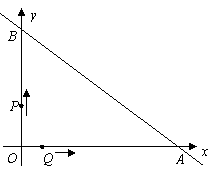 (3)当
(3)当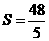 时,求出点
时,求出点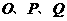 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点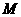 的坐标.
的坐标.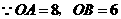
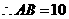
 点
点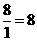 (秒)
(秒) 点
点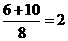 (单位/秒)·· 1分
(单位/秒)·· 1分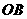 上运动(或0
上运动(或0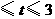 )时,
)时,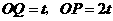
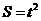 ··························································································································· 1分
··························································································································· 1分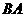 上运动(或
上运动(或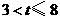 )时,
)时,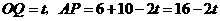 ,
,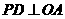 于点
于点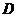 ,由
,由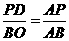 ,得
,得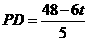 ,··································· 1分
,··································· 1分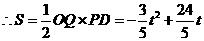 ·················································································· 1分
·················································································· 1分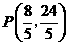 ··········································································································· 1分
··········································································································· 1分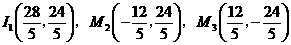 ···························································· 3分
···························································· 3分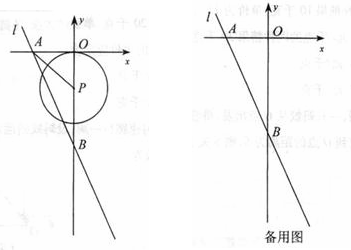
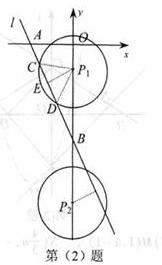 (2)设⊙P与直线l交于C,D两点,连结PC,PD当圆心P在线段OB上时,作PE⊥CD于E.
(2)设⊙P与直线l交于C,D两点,连结PC,PD当圆心P在线段OB上时,作PE⊥CD于E.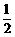 CD=
CD=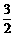 ,PD=3,
,PD=3,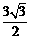 .
.
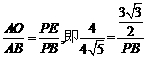 ,
,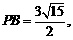
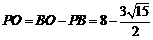 ,
,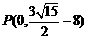 ,
,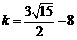 .
.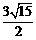 -8),
-8),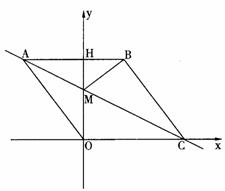

 5(09河北)在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
5(09河北)在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).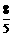 ;
; 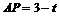 .
.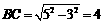 ,
, 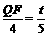 .∴
.∴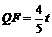 .
.  ∴
∴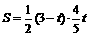 ,
,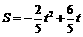 .
.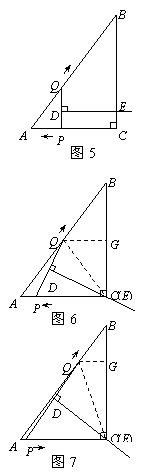 由△APQ ∽△ABC,得
由△APQ ∽△ABC,得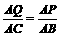 ,
,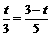 . 解得
. 解得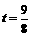 .
. 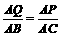 ,
,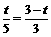 . 解得
. 解得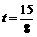 .
. 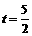 或
或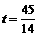 .
.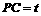 ,
,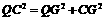
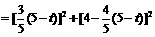 .
.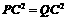 ,得
,得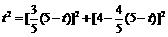 ,解得
,解得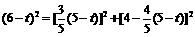 ,
,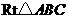 中,
中,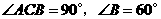 ,
, .点
.点 的中点,过点
的中点,过点 从与
从与
 边于点
边于点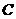 作
作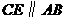 交直线
交直线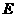 ,设直线
,设直线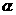 .
.
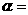 度时,四边形
度时,四边形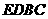 是等腰梯形,此时
是等腰梯形,此时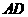 的长为 ;
的长为 ;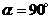 时,判断四边形
时,判断四边形 .
.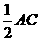 =
=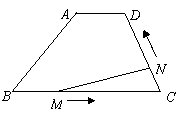 7(09济南)如图,在梯形
7(09济南)如图,在梯形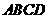 中,
中,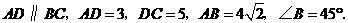 动点
动点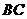 以每秒2个单位长度的速度向终点
以每秒2个单位长度的速度向终点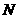 同时从
同时从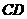 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点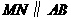 时,求
时,求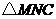 为等腰三角形.
为等腰三角形.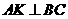 于
于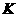 ,
,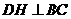 于
于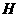 ,则四边形
,则四边形 是矩形
是矩形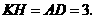 ····························································································· 1分
····························································································· 1分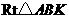 中,
中,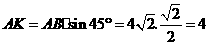
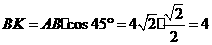 ···································································· 2分
···································································· 2分 中,由勾股定理得,
中,由勾股定理得,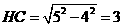
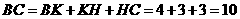 ························································· 3分
························································· 3分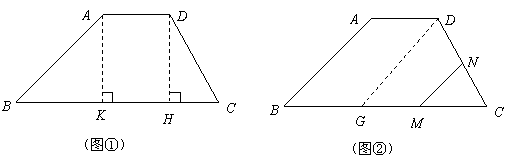
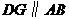 交
交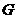 点,则四边形
点,则四边形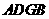 是平行四边形
是平行四边形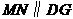
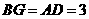
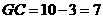 ·························································································· 4分
·························································································· 4分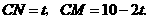
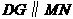
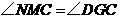
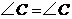
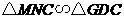
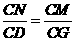 ································································································· 5分
································································································· 5分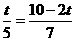
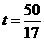 ·································································································· 6分
·································································································· 6分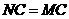 时,如图③,即
时,如图③,即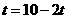
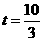 ········································································································· 7分
········································································································· 7分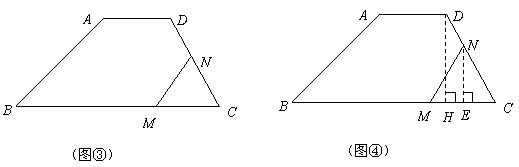
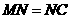 时,如图④,过
时,如图④,过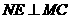 于
于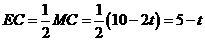
 中,
中,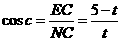
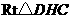 中,
中,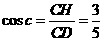
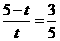
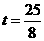 ····································································································· 8分
····································································································· 8分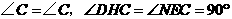
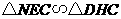
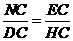
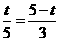
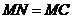 时,如图⑤,过
时,如图⑤,过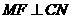 于
于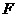 点.
点.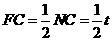
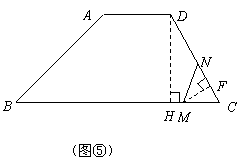
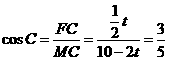
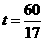
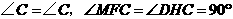
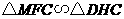
 ,
, 的中点,过点
的中点,过点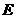 作
作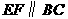 交
交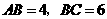 ,
,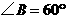 .
.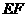 上的一个动点,过
上的一个动点,过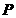 作
作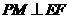 交
交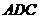 于点
于点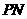 ,设
,设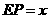 .
.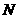 在线段
在线段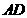 上时(如图2),
上时(如图2),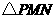 的形状是否发生改变?若不变,求出
的形状是否发生改变?若不变,求出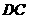 上时(如图3),是否存在点
上时(如图3),是否存在点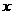 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.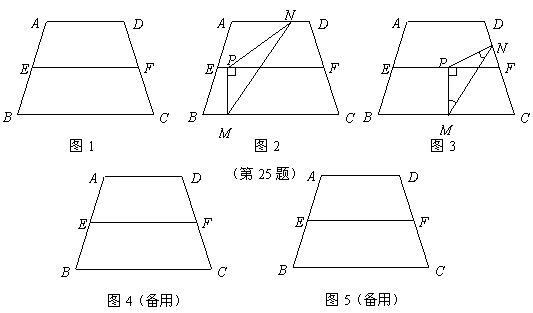
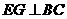 于点
于点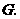 ························· 1分
························· 1分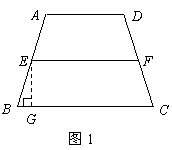 ∵
∵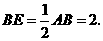
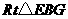 中,
中,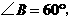 ∴
∴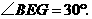 ············· 2分
············· 2分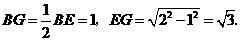
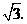 ··········································· 3分
··········································· 3分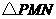 的形状不发生改变.
的形状不发生改变.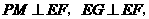 ∴
∴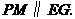
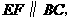 ∴
∴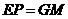 ,
,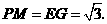
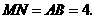 ······························································································· 4分
······························································································· 4分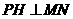 于
于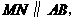
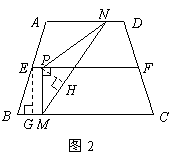 ∴
∴
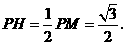
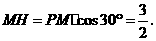
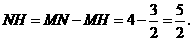
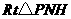 中,
中,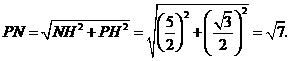
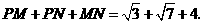 ············································· 6分
············································· 6分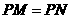 时,如图3,作
时,如图3,作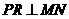 于
于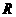 ,则
,则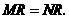
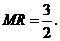
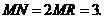 ································································································ 7分
································································································ 7分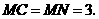
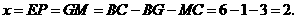 ········································· 8分
········································· 8分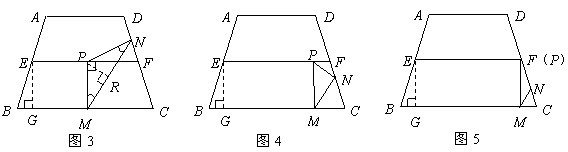
 当
当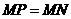 时,如图4,这时
时,如图4,这时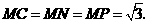
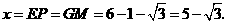
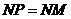 时,如图5,
时,如图5,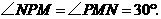
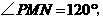 又
又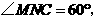
 为直角三角形.
为直角三角形.
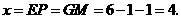
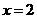 或4或
或4或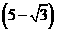 时,
时,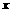 (长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;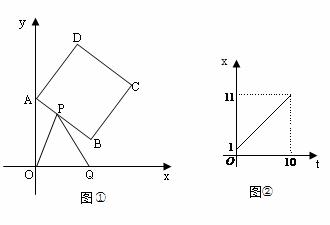
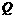 (1,0)···································································································· 1分
(1,0)···································································································· 1分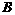 作BF⊥y轴于点
作BF⊥y轴于点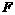 ,
,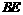 ⊥
⊥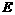 ,则
,则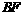 =8,
=8,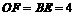 .
.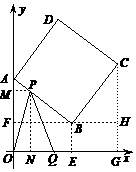 ∴
∴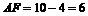 .
.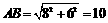 3分
3分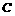 作
作 ⊥
⊥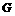 ,与
,与 的延长线交于点
的延长线交于点 .
.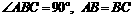 ∴△ABF≌△BCH.
∴△ABF≌△BCH. 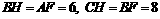 .
. 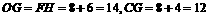 .
.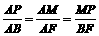 .
.
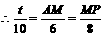 .
. 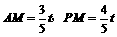 .
∴
.
∴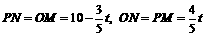 .
.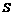 (平方单位)
(平方单位)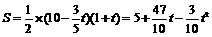 (0≤
(0≤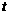 ≤10) ························································ 5分
≤10) ························································ 5分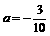 <0 ∴当
<0 ∴当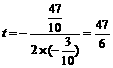 时, △OPQ的面积最大.······························ 6分
时, △OPQ的面积最大.······························ 6分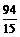 ,
,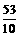 ) .················································································· 7分
) .················································································· 7分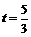 或
或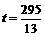 时,
OP与PQ相等.························································· 9分
时,
OP与PQ相等.························································· 9分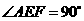 ,且EF交正方形外角
,且EF交正方形外角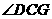 的平行线CF于点F,求证:AE=EF.
的平行线CF于点F,求证:AE=EF.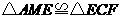 ,所以
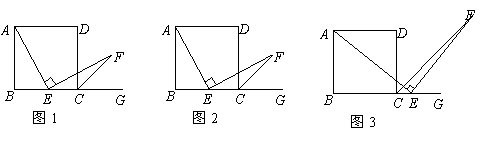
,所以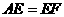 .
.
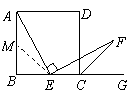 证明:在
证明:在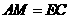 ,连接
,连接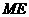 . (2分)
. (2分)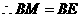 .
.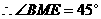 ,
,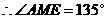 .
. 是外角平分线,
是外角平分线,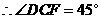 ,
,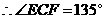 .
.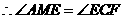 .
.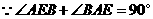 ,
,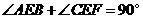 ,
,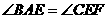 .
.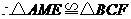 (ASA).············································································ (5分)
(ASA).············································································ (5分) .······································································································· (6分)
.······································································································· (6分) 使
使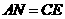 ,连接
,连接 .········································ (8分)
.········································ (8分) .
.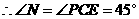 .
.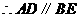 .
.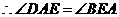 .
.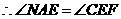 .
. (ASA).··········································································· (10分)
(ASA).··········································································· (10分) ,其中
,其中 .如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边
.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边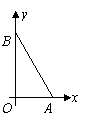 (Ⅰ)若折叠后使点
(Ⅰ)若折叠后使点 厘米,
厘米,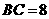 厘米,点
厘米,点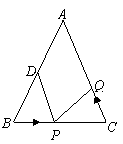 ①若点Q的运动速度与点P的运动速度相等,经过1秒后,
①若点Q的运动速度与点P的运动速度相等,经过1秒后,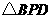 与
与 是否全等,请说明理由;
是否全等,请说明理由; 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在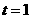 秒,
秒,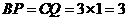 厘米,
厘米,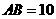 厘米,点
厘米,点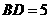 厘米.
厘米.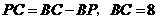 厘米,
厘米,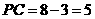 厘米,
厘米,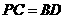 .
.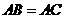 ,
,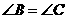 ,
,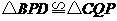 .·························································································· (4分)
.·························································································· (4分)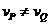 , ∴
, ∴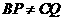 ,
,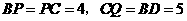 ,
,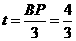 秒,
秒,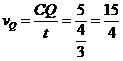 厘米/秒.············································································· (7分)
厘米/秒.············································································· (7分)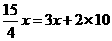 ,
,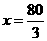 秒.
秒.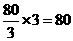 厘米.
厘米.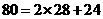 ,
,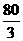 秒点
秒点