0 47593 47601 47607 47611 47617 47619 47623 47629 47631 47637 47643 47647 47649 47653 47659 47661 47667 47671 47673 47677 47679 47683 47685 47687 47688 47689 47691 47692 47693 47695 47697 47701 47703 47707 47709 47713 47719 47721 47727 47731 47733 47737 47743 47749 47751 47757 47761 47763 47769 47773 47779 47787 447348
 BO·AE
BO·AE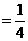 BO·DO·AE·CF
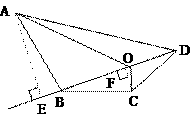
BO·DO·AE·CF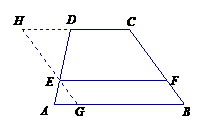 例4(江苏连云港)(1)如图5,在梯形ABCD中,AB∥CD,
例4(江苏连云港)(1)如图5,在梯形ABCD中,AB∥CD,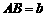 ,
,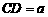 ,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实:
,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实: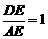 时,有
时,有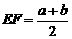 ;
;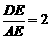 时,有
时,有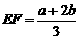 ;
;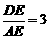 时,有
时,有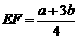 .
.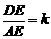 时,参照上述研究结论,请你猜想用k表示DE的一般结论,并给出证明;
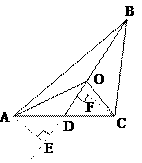
时,参照上述研究结论,请你猜想用k表示DE的一般结论,并给出证明;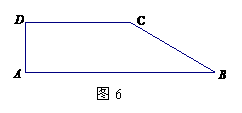 (2)现有一块直角梯形田地
(2)现有一块直角梯形田地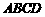 (如图6所示),其中AB∥CD,
(如图6所示),其中AB∥CD,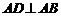 ,
,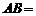 310米,
310米,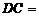 170米,
170米,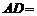 70米.若要将这块地分割成两块,由两农户来承包,要求这两块地均为直角梯形,且它们的面积相等.请你给出具体分割方案.
70米.若要将这块地分割成两块,由两农户来承包,要求这两块地均为直角梯形,且它们的面积相等.请你给出具体分割方案.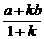 .
. ∽
∽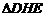 ,∴
,∴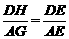 ,
,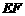 //
// //
// ,∴
,∴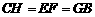 ,
,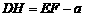 ,
,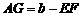 ,
,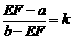 ,可得
,可得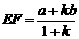 .
. 上取一点E,作EF∥AB交BC于点F,设
上取一点E,作EF∥AB交BC于点F,设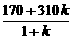 ,
,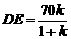 ,
, 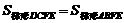 ,则
,则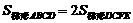 ,
,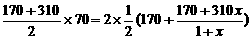
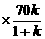 ,
, 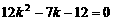 解得:
解得: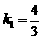 ,
,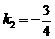 (舍去),
(舍去), 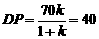 ,
,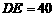 米,作EF∥AB(或
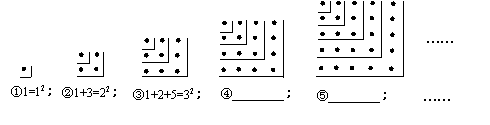
米,作EF∥AB(或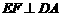 ),
), 例2(河北课改实验区)观察图2所示的点阵图和相应的等式,探究其中的规律:
例2(河北课改实验区)观察图2所示的点阵图和相应的等式,探究其中的规律: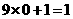 ;
;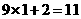 ;
;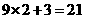 ;
;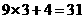 ;
;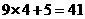 ;
;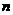 个等式(
个等式(
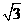 )在
)在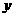 轴的正半轴上,A、B是
轴的正半轴上,A、B是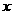 轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q.
轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q.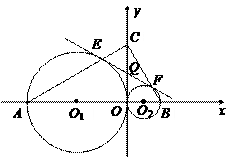
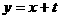 的图象
的图象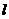 随
随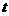 的不同取值变化时,位于
的不同取值变化时,位于 (阴影部分).
(阴影部分).