27.张明、王成两位同学初二学年10次数学单元自我检测的成绩(成绩均为整数,且个位数为0)分别如图所示:
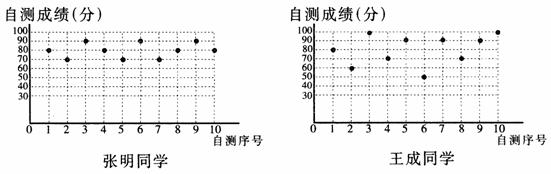
利用图中提供的信息,解答下列问题
(1)完成下表:
|
姓 名 |
平均成绩 |
中位数 |
众数 |
方差(S2) |
|
张 明 |
|
80 |
80 |
|
|
王 成 |
|
|
|
260 |
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率高的同学是 ;
(3)根据图表信息,请你对这两位同学各提一条不超过20个字的学习建议。
 -1
-1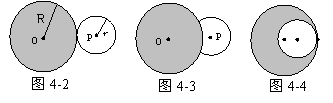 分析:从2时48分到3时52分共64分钟,点 P运动的路程为2r,
分析:从2时48分到3时52分共64分钟,点 P运动的路程为2r,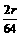 ,即
,即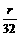 ,
,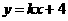 与函数
与函数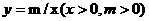 的图象交于A、B两点,且与x、y轴分别交于C、D两点.
的图象交于A、B两点,且与x、y轴分别交于C、D两点. 的面积是
的面积是 的面积的
的面积的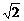 倍,求
倍,求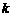 与
与 之间的函数关系式;
之间的函数关系式;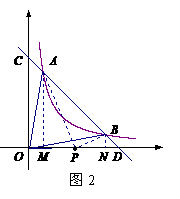 (2)在(1)的条件下,是否存在
(2)在(1)的条件下,是否存在 为直径的圆经过点
为直径的圆经过点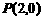 .若存在,求出
.若存在,求出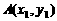 ,
,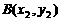 (其中
(其中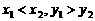 ),
),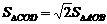 ,得
,得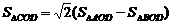
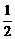 ·
· ·
·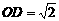 (
(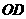 ·
·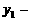
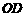 ·
·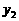 ),
),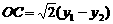 ,
, 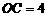 ,∴
,∴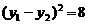 ,即
,即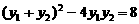 ,
,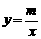 可得
可得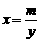 ,代入
,代入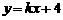 可得
可得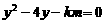 ①
①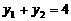 ,
,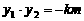 ,
, 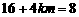 ,即
,即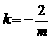 .
. 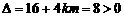 ,
,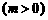 .
. 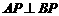 ,过
,过 、
、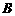 分别作
分别作 轴的垂线,垂足分别为
轴的垂线,垂足分别为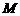 、
、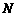 .
. 与
与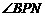 都与
都与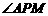 互余,∴
互余,∴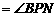 .
.  ∽Rt
∽Rt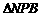 ,∴
,∴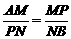 .
. 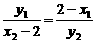 ,∴
,∴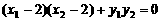 , ∴
, ∴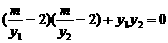 ,
,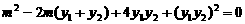 ②
② 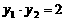 ,代入②得
,代入②得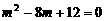 ,
,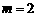 或
或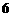 ,又
,又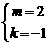 或
或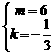 ,
,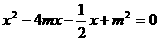 的两个实数根. 若D、E分别是BC、AC上的点,且∠ADE=60°,设BD=x,AE=y,求y关于x的函数关系式,并求出y的最小值.
的两个实数根. 若D、E分别是BC、AC上的点,且∠ADE=60°,设BD=x,AE=y,求y关于x的函数关系式,并求出y的最小值. 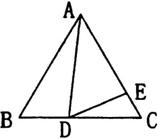
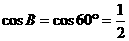
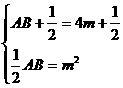
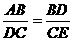
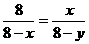
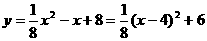
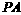 切⊙
切⊙ 于
于 ,割线
,割线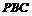 经过圆心
经过圆心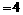 ,
,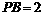 ,则
,则 的值为( )
的值为( )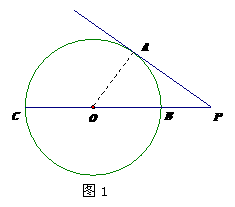 A.
A.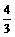 B.
B.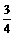 C.
C.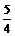 D.
D.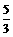
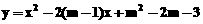 ,其中m为实数
,其中m为实数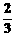 ,求这个二次函数的解析式。
,求这个二次函数的解析式。