摘要：猜想图形规律 根据一组相关图形的变化规律.从中总结通过图形的变化所反映的规律.其中.以图形为载体的数字规律最为常见.猜想这种规律.需要把图形中的有关数量关系列式表达出来.再对所列式进行对照.仿照猜想数式规律的方法得到最终结论. 例2观察图2所示的点阵图和相应的等式.探究其中的规律: 图2 (1)在④和⑤后面的横线上分别写出相应的等式, (2)通过猜想写出与第n个点阵相对应的等式. 分析:(1)本题图形中所反映出来的数字关系已经列出三个.下面就以它们为例.填写后两个.易得④1+3+5+7=42,⑤1+3+5+7+9=52. (2)仿照例1的思路可以猜想:1+3+5+-+=n2 .
网址：http://m.1010jiajiao.com/timu3_id_476907[举报]
附加题阅读、理解和探索
（1）观察下列各式：①
=1-
；②
=
-
；③
=
-
；…用你发现的规律写出：第④个式子是（ ），第n个式子是（ ）；
（2）利用（1）中的规律，计算：
+
+
+…+
；
（3）应用以上规律化简：
+
+
+…+
；
（4）观察按规律排列一组数：
，
，
，…，猜想第n个数是什么（请用含n的式子表达）把它填入求这组数的前n项和：
+
+
+…+（ ）中的括号内，并把这个和式化简．
查看习题详情和答案>>
（1）观察下列各式：①
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
（2）利用（1）中的规律，计算：
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
（3）应用以上规律化简：
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
| 1 |
| (n+2)(n+3) |
| 1 |
| (n+2008)(n+2009) |
（4）观察按规律排列一组数：
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
阅读、理解和探索
（1）观察下列各式：①
；②
；③
；…用你发现的规律写出：第④个式子是（______），第n个式子是（______）；
（2）利用（1）中的规律，计算：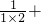
+
+
；
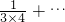（3）应用以上规律化简：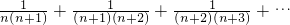
+
；
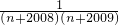（4）观察按规律排列一组数：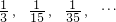
，猜想第n个数是什么（请用含n的式子表达）把它填入求这组数的前n项和：
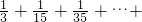（______）中的括号内，并把这个和式化简．
查看习题详情和答案>>
21、已知：如图，点D、E分别为△ABC的边AB、AC的中点，将△ADE绕点D旋转180°至△BDF．（1）小明发现四边形BCEF的形状是平行四边形，请你帮他把说理过程补齐．
理由是：因为△BDF是由△ADE绕点D旋转180°得到的所以△ADE与△BDF全等且点A、D、B在同一条直线上点E、D、F也在同一条直线上．
所以BF=AE，∠F=∠
AED
可得BF∥
AC
又因为E是AC的中点，所以EC=AE，
所以BF=
EC
因此，四边形BCEF是平行四边形（根据
一组对边平行切相等的四边形是平行四边形
）（2）小明还发现在原有的△ABC中添加一个条件后，就可以使四边形BFEC成为一种特殊的平行四边形．你也来试试．
你认为添加条件
∠C=90°
后，四边形BFEC是矩形
．（友情提示：我们将根据你所提出问题的难易程度，给予不同的分值．）理由是：有一个角是直角的平行四边形是矩形
．