|
|
 型利润 型利润 |
 型利润 型利润 |
|
甲店 |
200 |
170 |
|
乙店 |
160 |
150 |
(1)设分配给甲店 型产品
型产品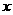 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为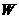 (元),求
(元),求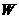 关于
关于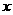 的函数关系式,并求出
的函数关系式,并求出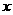 的取值范围;(3分)
的取值范围;(3分)
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;(4分)
(3)为了促销,公司决定仅对甲店 型产品让利销售,每件让利
型产品让利销售,每件让利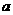 元,但让利后
元,但让利后 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店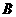 型产品的每件利润.甲店的
型产品的每件利润.甲店的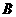 型产品以及乙店的
型产品以及乙店的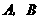 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?(3分)
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?(3分)
28.(10分)已知,在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2。若以O为坐标原点,OA所在直线为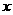 轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。
轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。
(1)求点C的坐标;(2分)
(2)若抛物线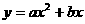 (
(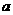 ≠0)经过C、A两点,求此抛物线的解析式;(3分)
≠0)经过C、A两点,求此抛物线的解析式;(3分)
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作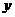 轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。(5分)
轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。(5分)
注:抛物线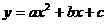 (
(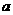 ≠0)的顶点坐标为
≠0)的顶点坐标为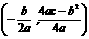 ,对称轴公式为
,对称轴公式为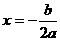
22.(10分)已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。求证:(1)△ABC≌△DEF;(2)GF=GC。
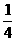 ;(2)
;(2)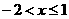 ;
;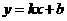 的图象与反比例函数
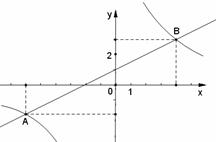
的图象与反比例函数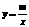 的图象相交于A、B两点。(1)根据图象,分别写出A、B的坐标;(3分)(2)求出两函数解析式;(4分)(3)根据图象回答:当
的图象相交于A、B两点。(1)根据图象,分别写出A、B的坐标;(3分)(2)求出两函数解析式;(4分)(3)根据图象回答:当
 (10分)如图,方格纸中有一条美丽可爱的小金鱼.(1)在同一方格纸中,画出将小金鱼图案绕原点O旋转180°后得的图案;(5分)(2)在同一方格纸中,并在
(10分)如图,方格纸中有一条美丽可爱的小金鱼.(1)在同一方格纸中,画出将小金鱼图案绕原点O旋转180°后得的图案;(5分)(2)在同一方格纸中,并在
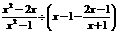 ,其中
,其中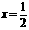 。
。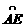 是劣弧
是劣弧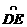 的2倍;⑤AE=BC。其中正确结论的序号是
。
的2倍;⑤AE=BC。其中正确结论的序号是
。