(一)方程与方程组 3一元二次方程
4方程组
5分式方程
6应用
1、 概念:方程、方程的解、解方程、方程组、方程组的解
2、 一元一次方程:
解方程的步骤:去分母、去括号、移项、合并同类项、系数化一(未知项系数不能为零)
例题:.解方程:
(1) 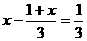 (2)
(2)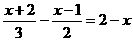
解:
(3)[05湘潭] 关于x的方程mx+4=3x+5的解是x=1,则m= 。
解:
3、一元二次方程:
(1)
一般形式: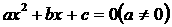
(2) 解法:
直接开平方法、因式分解法、配方法、公式法
求根公式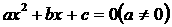
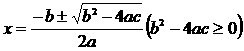
例题:
①、解下列方程:
(1)x2-2x=0; (2)45-x2=0;
(3)(1-3x)2=1; (4)(2x+3)2-25=0.
(5)(t-2)(t+1)=0; (6)x2+8x-2=0
(7 )2x2-6x-3=0; (8)3(x-5)2=2(5-x)
解:
② 填空:
(1)x2+6x+( )=(x+ )2;
(2)x2-8x+( )=(x- )2;
(3)x2+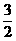 x+( )=(x+ )2
x+( )=(x+ )2
(3)判别式△=b²-4ac的三种情况与根的关系
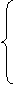
 当
当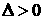 时
有两个不相等的实数根 ,
时
有两个不相等的实数根 ,
 当
当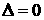 时
有两个相等的实数根
时
有两个相等的实数根
 当
当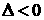 时
没有实数根。
时
没有实数根。
 当△≥0时 有两个实数根
当△≥0时 有两个实数根
例题.①.(无锡市)若关于x的方程x2+2x+k=0有两个相等的实数根,则k满足 ( )
A.k>1 B.k≥1 C.k=1 D.k<1
②(常州市)关于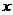 的一元二次方程
的一元二次方程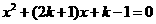 根的情况是( )
根的情况是( )
(A)有两个不相等实数根 (B)有两个相等实数根
(C)没有实数根 (D)根的情况无法判定
③.(浙江富阳市)已知方程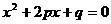 有两个不相等的实数根,则
有两个不相等的实数根,则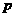 、
、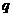 满足的关系式是( )
满足的关系式是( )
A、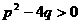 B、
B、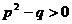 C、
C、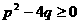 D、
D、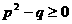
(4)根与系数的关系:x1+x2=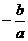 ,x1x2=
,x1x2=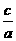
例题: (浙江富阳市)已知方程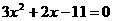 的两根分别为
的两根分别为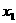 、
、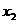 ,则
,则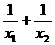 的值是( )
的值是( )
A、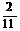 B、
B、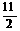 C、
C、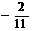 D、
D、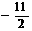
4、 方程组:
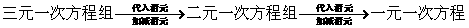
二元(三元)一次方程组的解法:代入消元、加减消元
例题:[05泸州]解方程组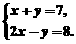
解
[05南京]解方程组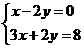
解
[05苏州]解方程组: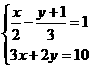
解
[05遂宁课改]解方程组: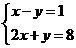
解
[05宁德]解方程组:
解
5、分式方程:
分式方程的解法步骤:
(1) 一般方法:选择最简公分母、去分母、解整式方程,检验
(2) 换元法
例题:①、解方程: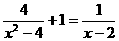 的解为
的解为
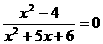 根为
根为
②、[北京市海淀区]当使用换元法解方程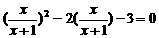 时,若设
时,若设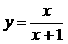 ,则原方程可变形为( )
,则原方程可变形为( )
A.y2+2y+3=0 B.y2-2y+3=0
C.y2+2y-3=0 D.y2-2y-3=0
(3)、用换元法解方程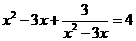 时,设
时,设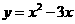 ,则原方程可化为( )
,则原方程可化为( )
(A)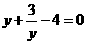 (B)
(B)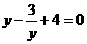 (C)
(C)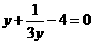 (D)
(D)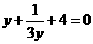
6、应用:
(1)分式方程(行程、工作问题、顺逆流问题)
(2)一元二次方程(增长率、面积问题)
(3)方程组实际中的运用
例题:①轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同.已知水流的速度是3千米/时,求轮船在静水中的速度.(提示:顺水速度=静水速度+水流速度,逆水速度=静水速度-水流速度)
解:
②乙两辆汽车同时分别从A、B两城沿同一条高速公路驶向C城.已知A、C两城的距离为450千米,B、C两城的距离为400千米,甲车比乙车的速度快10
千米/时,结果两辆车同时到达C城.求两车的速度
解
③某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解
④[05绵阳]已知等式 (2A-7B) x+(3A-8B)=8x+10对一切实数x都成立,求A、B的值
解
⑤[05南通]某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
|
捐款(元) |
1 |
 2 2 |
3 |
4 |
|
人 数 |
6 |
|
|
7 |
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2元的有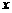 名同学,捐款3元的有
名同学,捐款3元的有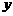 名同学,根据题意,可得方程组
名同学,根据题意,可得方程组
A、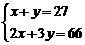 B、
B、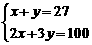 C、
C、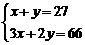 D、
D、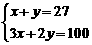
解
⑥已知三个连续奇数的平方和是371,求这三个奇数.
解
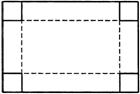 ⑦一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方米.求截去正方形的边长.
⑦一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方米.求截去正方形的边长.
解:
1几个概念
 知识结构及内容:
1几个概念
知识结构及内容:
1几个概念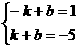
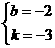 y=-3x-2
y=-3x-2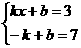
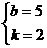
 y=-2x+5
y=-2x+5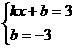
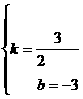
 x-3
x-3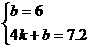
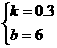 y=0.3x+6
y=0.3x+6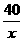 (3)s=100
(3)s=100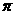 -
-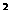 (0<r<10)
(0<r<10) 2
(4)x>-3
2
(4)x>-3