|
转动转盘的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
|
落在“铅笔”区域中的次数m |
68 |
111 |
136 |
352 |
556 |
701 |
落在“铅笔”区域中的频率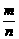 |
|
|
|
|
|
|
(2)当转动转盘的次数n很大时,概率将会接近多少?
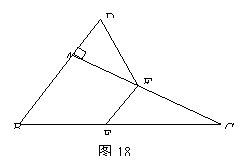
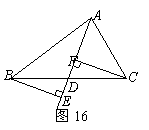
24,如图16,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断AD是△ABC的中线还是角平分线?请说明你判断的理由. 25,如图17,某学校九年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让一名5岁小朋友小军从最外环任一个进口进入.(1)小军能进入迷宫中心的概率是多少?请画出树状图进行说明.(2)小组两位组员小张和小李商量做一个小游戏,以猜测小军进迷宫的结果比胜负.游戏规则规完:小军如果能进入迷宫中心,小张和小李各得1分;小军如果不能进入迷宫中心,则他在最后一个进口处所得乘积是奇数时,小张得3分,所得乘积是偶数时,小李得3分,你认为这个游戏公平吗?如果公平,请说明理由;如果不公平,请在第二道环进口处的两个数中改变其中一个数使游戏公平.(3)在(2)的游戏规则下,让小军从最外环进口任意进入10次,最终小张和小李的总得分之和不超过28分,请问小军至少几次进入迷宫中心?

 26,如图18,已知:在△ABC中,∠BAC=90°,延长BA到点D,使AD=
26,如图18,已知:在△ABC中,∠BAC=90°,延长BA到点D,使AD=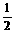 AB,点G、E、F分别为边AB、BC、AC的中点.求证:DF=BE.
AB,点G、E、F分别为边AB、BC、AC的中点.求证:DF=BE.
27,2008年5月,第六届中国某市国际龙舟拉力赛在该市揭开比赛帷幕.20日上午9时,参赛龙舟从该市同时出发.其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图19所示.甲队在上午11时30分到达终点某市河港.(1)哪个队先到达终点?乙队何时追上甲队?(2)在比赛过程中,甲、乙两队何时相距最远?
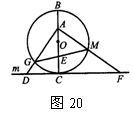
28,如图20,⊙O的直径BC=4,过点C作⊙O的切线m,D是直线m上一点,且DC=2,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AD的垂线交直线m于点F,交⊙O于点H,连结GH交BC于点E.(1)当A是BO的中点时,求AF的长;(2)若∠AGH=∠AFD,求△AGH的面积.
29,已知二次函数y=ax2+bx+c.(1)若a=2,c=-3,且二次函数的图像经过点(-1,-2),求b的值;(2)若a=2,b+c=-2,b>c,且二次函数的图像经过点(p,-2),求证:b≥0;(3)若a+b+c=0,a>b>c,且二次函数的图像经过点(q,-a),试问当自变量x=q +4时,二次函数y=ax2+bx+c所对应的函数值y是否大于0?请证明你的结论.
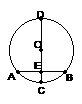 圆是中心对称图形,对称中心为
.
圆是中心对称图形,对称中心为
.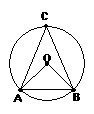 (1)图中的圆心角
;圆周角
;
(1)图中的圆心角
;圆周角
; 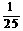 .
.

 15,母亲节那天,很多同学给妈妈准备了鲜花和礼盒.从如图11中信息可知一束鲜花的价格是___元.
15,母亲节那天,很多同学给妈妈准备了鲜花和礼盒.从如图11中信息可知一束鲜花的价格是___元. 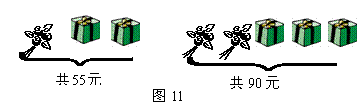
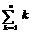 =1+2+3+…+(n-1)+ n.1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n-1)×(n-2)×…×3×2×1.则
=1+2+3+…+(n-1)+ n.1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n-1)×(n-2)×…×3×2×1.则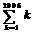 -
-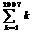 +
+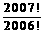 =___.
=___. (本题9分)如图,已知直线
(本题9分)如图,已知直线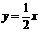 与双曲线
与双曲线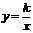 (k>0)交于A、B两点,且A点的横坐标为4. (1)求k的值;(2)若双曲线
(k>0)交于A、B两点,且A点的横坐标为4. (1)求k的值;(2)若双曲线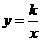 (k>0)上一点C的纵坐标为8,求△AOC的面积。
(k>0)上一点C的纵坐标为8,求△AOC的面积。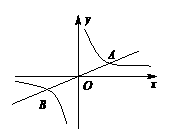
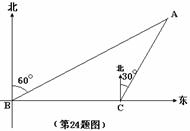
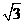 =1.732)
=1.732)