0 44690 44698 44704 44708 44714 44716 44720 44726 44728 44734 44740 44744 44746 44750 44756 44758 44764 44768 44770 44774 44776 44780 44782 44784 44785 44786 44788 44789 44790 44792 44794 44798 44800 44804 44806 44810 44816 44818 44824 44828 44830 44834 44840 44846 44848 44854 44858 44860 44866 44870 44876 44884 447348
 =x2(1-
=x2(1- +
+ )
) n-m)元/分钟
B.(
n-m)元/分钟
B.(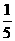 n-m)元/分钟
D.(
n-m)元/分钟
D.(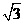 是同类二次根式的是( )
是同类二次根式的是( )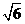 B.
B.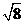 C.
C.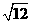 D.
D.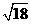
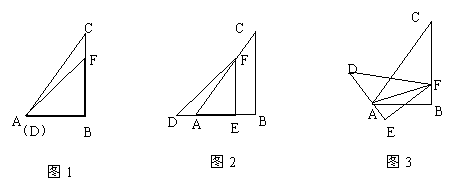
 。
。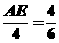 ,AE=
,AE= ,∴BE=AB-AE=4-
,∴BE=AB-AE=4-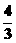
 (2)当t为何值时,以B,P,Q三点为顶点的三角形是
(2)当t为何值时,以B,P,Q三点为顶点的三角形是 解:(1)首先0≤t≤16,如图,过点P作PM⊥BC,垂足为M,
解:(1)首先0≤t≤16,如图,过点P作PM⊥BC,垂足为M,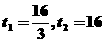 (不合题意,舍去)。综上可知,答案为t=3.5或
(不合题意,舍去)。综上可知,答案为t=3.5或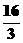 秒。
秒。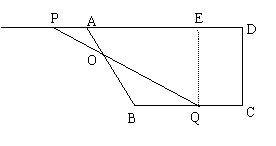 (3)如图,由△OAP∽△OBQ,得
(3)如图,由△OAP∽△OBQ,得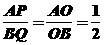 .
.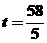 ,
,
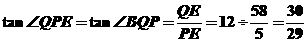
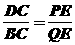 ,即
,即

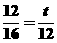 ,解得t=9。所以当t=9秒时,PQ⊥BD。
,解得t=9。所以当t=9秒时,PQ⊥BD。 如图,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括A和C),设AP=x,四边形PBCD的面积为y,
如图,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括A和C),设AP=x,四边形PBCD的面积为y,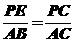 ,即
,即 ,PE=8-
,PE=8-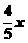 ,∴△PBC面积=
,∴△PBC面积=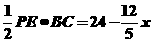 ,又△PCD面积=△PBC面积,∴y=
,又△PCD面积=△PBC面积,∴y=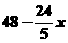 (0<x<10)
(0<x<10)
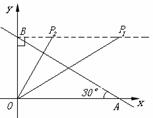
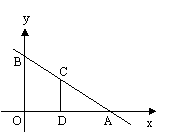 3、如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,
3、如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,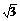 )两点,点C为线段AB上的一动点,过点C作CD⊥
)两点,点C为线段AB上的一动点,过点C作CD⊥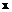 轴于点D。
轴于点D。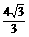 ,求点C的坐标;
,求点C的坐标;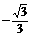 x+
x+ ,
, =
=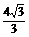 ,∴
,∴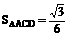
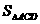 =
=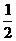 CD×AD=
CD×AD=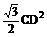 =
=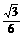 ,可得CD=
,可得CD=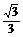 。
。 ∴AD=1,OD=2.∴C(2,
∴AD=1,OD=2.∴C(2,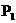 (3,
(3,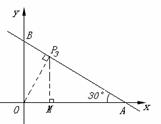 ② 若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=
② 若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=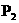 (1,
(1,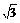 )。
)。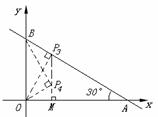 在Rt△PBO中,BP=
在Rt△PBO中,BP=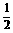 OB=
OB=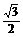 ,OP=
,OP=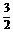 。
。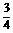 ;PM=
;PM=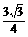 .∴
.∴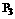 (
(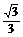 OM=
OM=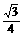 。∴
。∴ (
(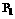 (3,
(3, (1,
(1, ),
), )。
)。