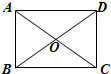
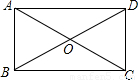
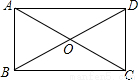
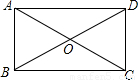
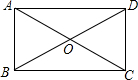
摘要：如图.矩形ABCD中.AB=8.BC=6.对角线AC上有一个动点P.设AP=x.四边形PBCD的面积为y. (1)写出y与x的函数关系.并确定自变量x的范围. (2)有人提出一个判断“关于动点P.△PBC面积与 △PAD面积之和为常. 请说明此判断是否正确.并说明理由. (3)将题目中的矩形改为平行四边形.且已知平行四边形的面积为S.对角线上一动点P.是否有“△PBC面积与△PAD面积之和为常 .并说明理由. 解:(1)过点P作PE⊥BC于点E.在Rt△ABC中.AC=10.PC=AC-AP=10-x.∵PE⊥BC.AB⊥BC,∴△PEC∽△ABC.则,即.PE=8-.∴△PBC面积=.又△PCD面积=△PBC面积.∴y= (2)这个判断是正确的.S△PBC+S△PAD=24,(3)有.S△PBC+S△PAD= 3.如图.平面直角坐标系中.直线AB与x轴.y轴分别交于A(3,0),B(0,)两点.点C为线段AB上的一动点.过点C作CD⊥轴于点D. (1) 写直线AB的解析式, (2) 若S梯形OBCD＝.求点C的坐标, (3) 在第一象限内是否存在点P.使得以P.O.B为顶点 的三角形与△OBA相似.若存在.请求出所有符合条件的点P的坐标,若不存在,请说明理由. 解:(1)直线AB解析式为:y=x+ (2)∵,＝.∴ 由OA=OB.得∠BAO＝30°.AD=CD. ∴＝CD×AD＝＝.可得CD＝. ∴AD=1.OD＝2．∴C(2.). (3)当∠OBP＝Rt∠时.如图 ①若△BOP∽△OBA.则∠BOP＝∠BAO=30°.BP=OB=3. ∴(3.). ② 若△BPO∽△OBA.则∠BPO＝∠BAO=30°,OP=OB=1. ∴(1.). 当∠OPB＝Rt∠时. ③ 过点P作OP⊥BC于点P.此时△PBO∽△OBA. ∠BOP＝∠BAO＝30°.过点P作PM⊥OA于点M. 在Rt△PBO中.BP＝OB＝.OP＝BP＝. ∵ 在Rt△PMO中.∠OPM＝30°. ∴ OM＝OP＝,PM＝OM＝．∴(.)． ④ 若△POB∽△OBA.则∠OBP=∠BAO＝30°.∠POM＝30°. ∴PM＝OM＝.∴(.)(由对称性也可得到点的坐标). 当∠OPB＝Rt∠时.点P在x轴上.不符合要求. 综合得.符合条件的点有四个.分别是:(3,),(1,),(,),(,).

网址：http://m.1010jiajiao.com/timu3_id_447871[举报]