0 138673 138681 138687 138691 138697 138699 138703 138709 138711 138717 138723 138727 138729 138733 138739 138741 138747 138751 138753 138757 138759 138763 138765 138767 138768 138769 138771 138772 138773 138775 138777 138781 138783 138787 138789 138793 138799 138801 138807 138811 138813 138817 138823 138829 138831 138837 138841 138843 138849 138853 138859 138867 447348
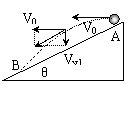 [例2]如图在倾角为θ的斜面顶端A处以速度V0水平抛出一小球,落在斜面上的某一点B处,设空气阻力不计,求(1)小球从A运动到B处所需的时间;(2)从抛出开始计时,经过多长时间小球离斜面的距离达到最大?
[例2]如图在倾角为θ的斜面顶端A处以速度V0水平抛出一小球,落在斜面上的某一点B处,设空气阻力不计,求(1)小球从A运动到B处所需的时间;(2)从抛出开始计时,经过多长时间小球离斜面的距离达到最大?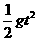 ,
由数学关系得到:
,
由数学关系得到: 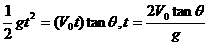
 (2)从抛出开始计时,经过t1时间小球离斜面的距离达到最大,当小球的速度与斜面平行时,小球离斜面的距离达到最大。因Vy1=gt1=V0tanθ,所以
(2)从抛出开始计时,经过t1时间小球离斜面的距离达到最大,当小球的速度与斜面平行时,小球离斜面的距离达到最大。因Vy1=gt1=V0tanθ,所以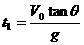
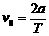 竖直方向:
竖直方向: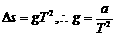
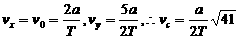
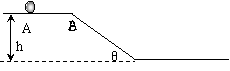 [例4]如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以V0=5m/s的速度在平面上向右运动。求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2)。某同学对此题的解法为:小球沿斜面运动,则
[例4]如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以V0=5m/s的速度在平面上向右运动。求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2)。某同学对此题的解法为:小球沿斜面运动,则 由此可求得落地的时间t。问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果。
由此可求得落地的时间t。问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果。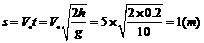
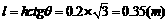
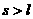 ,所以小球离开A点后不会落到斜面,因此落地时间即为平抛运动时间。
,所以小球离开A点后不会落到斜面,因此落地时间即为平抛运动时间。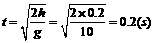
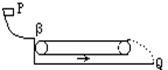 [例1] 物块从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带以后落到地面上的Q点,若传送带的皮带轮沿逆时针方向转动起来,使传送带随之运动,如图所示,再把物块放到P点自由滑下则
[例1] 物块从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带以后落到地面上的Q点,若传送带的皮带轮沿逆时针方向转动起来,使传送带随之运动,如图所示,再把物块放到P点自由滑下则 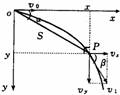 (2)平抛运动的处理方法:平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动。水平方向和竖直方向的两个分运动既具有独立性,又具有等时性.
(2)平抛运动的处理方法:平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动。水平方向和竖直方向的两个分运动既具有独立性,又具有等时性.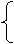
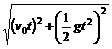 =
=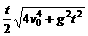 ,
, ,
,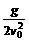 ·x2, 可见,平抛物体运动的轨迹是一条抛物线.
·x2, 可见,平抛物体运动的轨迹是一条抛物线.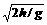 ,水平距离x=v0t=v0
,水平距离x=v0t=v0 ,水平发出,落在球台的P1点(如图实线所示),求P1点距O点的距离x1。.
,水平发出,落在球台的P1点(如图实线所示),求P1点距O点的距离x1。. 水平发出,恰好在最高点时越过球网落在球台的P2(如图虚线所示),求
水平发出,恰好在最高点时越过球网落在球台的P2(如图虚线所示),求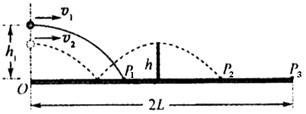
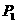 点与O点的距离
点与O点的距离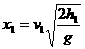 ;
;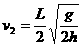 ;
;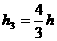
 ①
① ②
②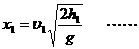 ③
③ ④
④ ⑤
⑤ ⑧
⑧ ⑨
⑨ ⑩
⑩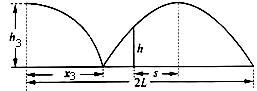
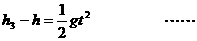 ⑿
⑿ ⒀
⒀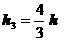
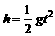 ①
①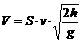 ④
④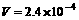 m3
⑤
m3
⑤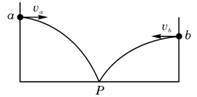 如图,在同一竖直面内,小球a、b从高度不同的两点,分别以初速度va和vb沿水平方向抛出,经过时间ta和tb后落到与两出点水平距离相等的P点。若不计空气阻力,下列关系式正确的是
如图,在同一竖直面内,小球a、b从高度不同的两点,分别以初速度va和vb沿水平方向抛出,经过时间ta和tb后落到与两出点水平距离相等的P点。若不计空气阻力,下列关系式正确的是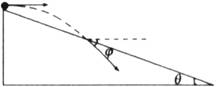 如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上。物体与斜面接触时速度与水平方向的夹角φ满足
如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上。物体与斜面接触时速度与水平方向的夹角φ满足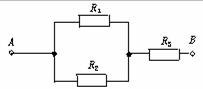
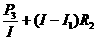 =9 V,代入数据得I=5 A,
R3=
=9 V,代入数据得I=5 A,
R3=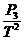 =0.6 Ω,
=0.6 Ω,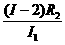 =3 Ω.
=3 Ω.