0 137547 137555 137561 137565 137571 137573 137577 137583 137585 137591 137597 137601 137603 137607 137613 137615 137621 137625 137627 137631 137633 137637 137639 137641 137642 137643 137645 137646 137647 137649 137651 137655 137657 137661 137663 137667 137673 137675 137681 137685 137687 137691 137697 137703 137705 137711 137715 137717 137723 137727 137733 137741 447348


 如图甲所示,一物体放置在倾角为θ的斜面上,斜面固定于加速上升的电梯中,加速度为a.在物体始终相对斜面静止的情况下,下列说法正确的是( )
如图甲所示,一物体放置在倾角为θ的斜面上,斜面固定于加速上升的电梯中,加速度为a.在物体始终相对斜面静止的情况下,下列说法正确的是( )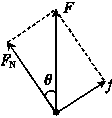 解法一 物体随电梯加速上升,斜面对物体的作用力F=m(g+a)
解法一 物体随电梯加速上升,斜面对物体的作用力F=m(g+a)
 如图所示,光滑水平地面上的小车的质量为M,站在小车水平底板上的人的质量为m,且m≠M.人用一根跨过定滑轮的绳子拉小车,定滑轮上下两侧的绳子都保持水平,不计绳与滑轮之间的摩擦.关于人和车一起向右加速运动的过程,下列说法正确的是( )
如图所示,光滑水平地面上的小车的质量为M,站在小车水平底板上的人的质量为m,且m≠M.人用一根跨过定滑轮的绳子拉小车,定滑轮上下两侧的绳子都保持水平,不计绳与滑轮之间的摩擦.关于人和车一起向右加速运动的过程,下列说法正确的是( )
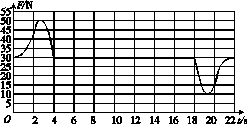
 A.小球将开始做自由落体运动
A.小球将开始做自由落体运动 a==g.
a==g. 如图所示,小球B放在真空容器A内,球B的直径恰好等于A的正方形空腔的边长,将它们以初速度v0竖直向上抛出,下列说法正确的是( )
如图所示,小球B放在真空容器A内,球B的直径恰好等于A的正方形空腔的边长,将它们以初速度v0竖直向上抛出,下列说法正确的是( )