0 136730 136738 136744 136748 136754 136756 136760 136766 136768 136774 136780 136784 136786 136790 136796 136798 136804 136808 136810 136814 136816 136820 136822 136824 136825 136826 136828 136829 136830 136832 136834 136838 136840 136844 136846 136850 136856 136858 136864 136868 136870 136874 136880 136886 136888 136894 136898 136900 136906 136910 136916 136924 447348

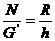 ,
, 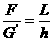
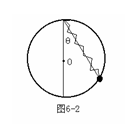 由于在拉动过程中,R、h不变,绳长L在减小,可见:球面的支持力
由于在拉动过程中,R、h不变,绳长L在减小,可见:球面的支持力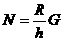 大小不变,绳子的拉力
大小不变,绳子的拉力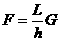 在减小。
在减小。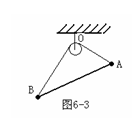 提示:可利用正弦定律求解或三角形相似法求解
提示:可利用正弦定律求解或三角形相似法求解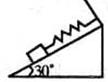 针对训练
针对训练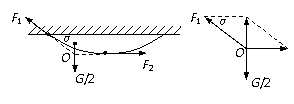 [例13]重G的均匀绳两端悬于水平天花板上的A、B两点。静止时绳两端的切线方向与天花板成α角。求绳的A端所受拉力F1和绳中点C处的张力F2。
[例13]重G的均匀绳两端悬于水平天花板上的A、B两点。静止时绳两端的切线方向与天花板成α角。求绳的A端所受拉力F1和绳中点C处的张力F2。
 解:以AC段绳为研究对象,根据判定定理,虽然AC所受的三个力分别作用在不同的点(如图中的A、C、P点),但它们必为共点力。设它们延长线的交点为O,用平行四边形定则作图可得:
解:以AC段绳为研究对象,根据判定定理,虽然AC所受的三个力分别作用在不同的点(如图中的A、C、P点),但它们必为共点力。设它们延长线的交点为O,用平行四边形定则作图可得: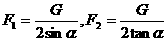
 7 解答平衡问题时常用的数学方法
7 解答平衡问题时常用的数学方法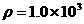 kg/m3,重力加速度为
kg/m3,重力加速度为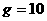 m/s2。求半径r=0.10mm的球形雨滴在无风情况下的稳态速度。
m/s2。求半径r=0.10mm的球形雨滴在无风情况下的稳态速度。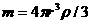 ,求得
,求得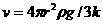 ,v=1.2m/s。
,v=1.2m/s。 隔离法:物体之间总是相互作用的,为了使研究的问题得到简化,常将研究对象从相互作用的物体中隔离出来,而其它物体对研究对象的影响一律以力来表示的研究方法叫隔离法。
隔离法:物体之间总是相互作用的,为了使研究的问题得到简化,常将研究对象从相互作用的物体中隔离出来,而其它物体对研究对象的影响一律以力来表示的研究方法叫隔离法。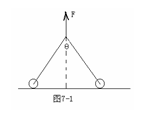
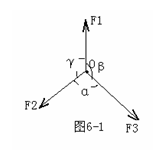
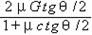 例10图7-1所示,两个完全相同重为G的球,两球与水平面间的动摩擦因数都是μ,一根轻绳两端固结在两个球上,在绳的中点施一个竖直向上的拉力,当绳被拉直后,两段绳间的夹角为θ。问当F至少多大时,两球将发生滑动?
例10图7-1所示,两个完全相同重为G的球,两球与水平面间的动摩擦因数都是μ,一根轻绳两端固结在两个球上,在绳的中点施一个竖直向上的拉力,当绳被拉直后,两段绳间的夹角为θ。问当F至少多大时,两球将发生滑动?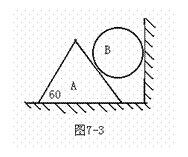
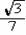 例11图7-3所示,光滑的金属球B放在纵截面为等腰三角形的物体A与竖直墙壁之间,恰好匀速下滑,已知物体A的重力是B的重力的6倍,不计球跟斜面和墙壁之间摩擦,问:物体A与水平面之间的动摩擦因数μ是多少?
例11图7-3所示,光滑的金属球B放在纵截面为等腰三角形的物体A与竖直墙壁之间,恰好匀速下滑,已知物体A的重力是B的重力的6倍,不计球跟斜面和墙壁之间摩擦,问:物体A与水平面之间的动摩擦因数μ是多少?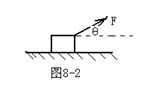 极限分析法:通过恰当地选取某个物理量推向极端(“极大”、“极小”、“极左”、“极右”)从而把比较隐蔽的临界现象(“各种可能性”)暴露出来,便于解答。
极限分析法:通过恰当地选取某个物理量推向极端(“极大”、“极小”、“极左”、“极右”)从而把比较隐蔽的临界现象(“各种可能性”)暴露出来,便于解答。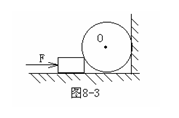 )
)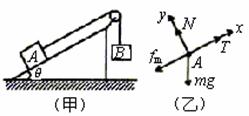 [例7跨过定滑轮的轻绳两端,分别系着物体A和物体B,物体A放在倾角为θ的斜面上(如图l-4-3(甲)所示),已知物体A的质量为m ,物体A与斜面的动摩擦因数为μ(μ<tanθ),滑轮的摩擦不计,要使物体A静止在斜面上,求物体B的质量的取值范围。
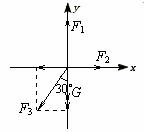
[例7跨过定滑轮的轻绳两端,分别系着物体A和物体B,物体A放在倾角为θ的斜面上(如图l-4-3(甲)所示),已知物体A的质量为m ,物体A与斜面的动摩擦因数为μ(μ<tanθ),滑轮的摩擦不计,要使物体A静止在斜面上,求物体B的质量的取值范围。 [例8 用与竖直方向成α=30°斜向右上方,大小为F的推力把一个重量为G的木块压在粗糙竖直墙上保持静止。求墙对木块的正压力大小N和墙对木块的摩擦力大小f。
[例8 用与竖直方向成α=30°斜向右上方,大小为F的推力把一个重量为G的木块压在粗糙竖直墙上保持静止。求墙对木块的正压力大小N和墙对木块的摩擦力大小f。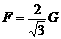 时,f=0;当
时,f=0;当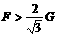 时,
时,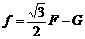 ,方向竖直向下;当
,方向竖直向下;当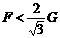 时,
时,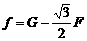 ,方向竖直向上。
,方向竖直向上。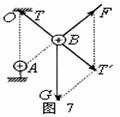
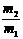 为A
为A B.
B.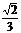 C.
C. D.
D.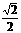

 物体在三个互不平行的力的作用下处于平衡,则这三个力必为共点力。(表示这三个力的矢量首尾相接,恰能组成一个封闭三角形)
物体在三个互不平行的力的作用下处于平衡,则这三个力必为共点力。(表示这三个力的矢量首尾相接,恰能组成一个封闭三角形) N 2
N 2