0 135558 135566 135572 135576 135582 135584 135588 135594 135596 135602 135608 135612 135614 135618 135624 135626 135632 135636 135638 135642 135644 135648 135650 135652 135653 135654 135656 135657 135658 135660 135662 135666 135668 135672 135674 135678 135684 135686 135692 135696 135698 135702 135708 135714 135716 135722 135726 135728 135734 135738 135744 135752 447348
 例
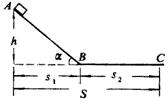
如图所示,小滑块从斜面顶点4由静止滑至水平部分C点而停止.已知斜面高为h,滑块运动的整个水平距离为s.求小滑块与接触面间的动摩擦因数(设滑块与各部分的动摩擦因数相同).
例
如图所示,小滑块从斜面顶点4由静止滑至水平部分C点而停止.已知斜面高为h,滑块运动的整个水平距离为s.求小滑块与接触面间的动摩擦因数(设滑块与各部分的动摩擦因数相同).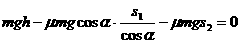
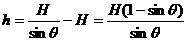
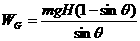
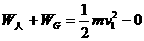
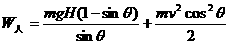
 例
质量为M的列车,沿平直轨道匀速前进,质量为m的末节车厢中途脱钩,当司机发觉时,机车已行驶L距离,于是他立即关闭油门,撤去牵引力。设车运动的阻力与重力成正比,机车的牵引力为定值,当列车的两部分都停止运动时,它们的距离是多少?
例
质量为M的列车,沿平直轨道匀速前进,质量为m的末节车厢中途脱钩,当司机发觉时,机车已行驶L距离,于是他立即关闭油门,撤去牵引力。设车运动的阻力与重力成正比,机车的牵引力为定值,当列车的两部分都停止运动时,它们的距离是多少? Δs=s1-s2=ML/(M-m)
Δs=s1-s2=ML/(M-m) 由于牵引力F=P/v,随着速度v的增大,牵引力F减小,则加速度a=(F-f)/m减小,但因a与v同向,汽车的速度v不断增大,F减小,a减小,直至a=0时,汽车作匀速运动,此时速度为最大值vm=P/F=P/f,在此之前,由牛顿第二定律得:(P/v)-f=ma,可知任一速度值均有与之相对应的一个确定的加速度值.由于汽车做变加速运动,所以不能用匀变速直线运动的公式求解,也不能对全过程应用牛顿第二定律,但动能定理是适用的,力和加速度瞬时对应关系也成立,因此解题时通常是对某一过程列动能定理方程,对某一瞬时列牛顿第二定律方程.
由于牵引力F=P/v,随着速度v的增大,牵引力F减小,则加速度a=(F-f)/m减小,但因a与v同向,汽车的速度v不断增大,F减小,a减小,直至a=0时,汽车作匀速运动,此时速度为最大值vm=P/F=P/f,在此之前,由牛顿第二定律得:(P/v)-f=ma,可知任一速度值均有与之相对应的一个确定的加速度值.由于汽车做变加速运动,所以不能用匀变速直线运动的公式求解,也不能对全过程应用牛顿第二定律,但动能定理是适用的,力和加速度瞬时对应关系也成立,因此解题时通常是对某一过程列动能定理方程,对某一瞬时列牛顿第二定律方程.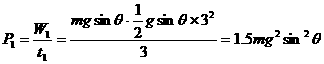

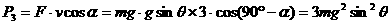
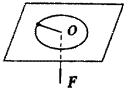 求解某个变力所做的功,可以利用动能定理,通过动能改变量和其余力做功情况来确定。
求解某个变力所做的功,可以利用动能定理,通过动能改变量和其余力做功情况来确定。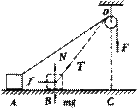 例
如图,用F=20N的恒力拉跨过定滑轮的细绳的一端,使质量为10kg的物体从A点由静止沿水平面运动.当它运动到B点时,速度为3m/s.设OC=4m,BC=3m,AC=9.6m,求物体克服摩擦力做的功.
例
如图,用F=20N的恒力拉跨过定滑轮的细绳的一端,使质量为10kg的物体从A点由静止沿水平面运动.当它运动到B点时,速度为3m/s.设OC=4m,BC=3m,AC=9.6m,求物体克服摩擦力做的功.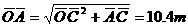
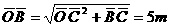
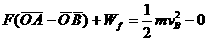
 [例]如图,密度为ρ,边长为a的正立方体木块漂浮在水面上(水的密度为ρ0).现用力将木块按入水中,直到木块上表面刚浸没,此过程浮力做了多少功?
[例]如图,密度为ρ,边长为a的正立方体木块漂浮在水面上(水的密度为ρ0).现用力将木块按入水中,直到木块上表面刚浸没,此过程浮力做了多少功?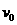 射
射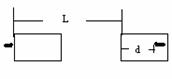 中与木块一起以速度v运动,已知当子弹相对木块静止时,木块前进距离为L,子弹进入木块的深度为d,若木块对子弹的阻力F恒定,那么下列关系式中正确的是( )、、
中与木块一起以速度v运动,已知当子弹相对木块静止时,木块前进距离为L,子弹进入木块的深度为d,若木块对子弹的阻力F恒定,那么下列关系式中正确的是( )、、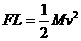 B、
B、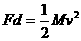
 D、
D、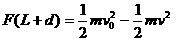
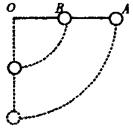 解 A、B两球组成的系统的机械能守恒,由机械能守恒定律:
解 A、B两球组成的系统的机械能守恒,由机械能守恒定律: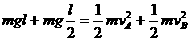
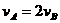
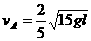 ,
,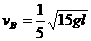
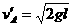 ,
,

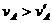 ,
,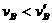 ,故杆对A球做正功,对B球做负功。
,故杆对A球做正功,对B球做负功。 例
如图示,质量为m、初速为v0的小木块,在桌面上滑动。动摩擦因数为μ,求木块停止滑动前摩擦力对木块和桌面所做的功。
例
如图示,质量为m、初速为v0的小木块,在桌面上滑动。动摩擦因数为μ,求木块停止滑动前摩擦力对木块和桌面所做的功。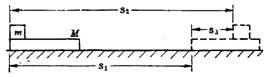 对桌面:W2=0
对桌面:W2=0