0 135556 135564 135570 135574 135580 135582 135586 135592 135594 135600 135606 135610 135612 135616 135622 135624 135630 135634 135636 135640 135642 135646 135648 135650 135651 135652 135654 135655 135656 135658 135660 135664 135666 135670 135672 135676 135682 135684 135690 135694 135696 135700 135706 135712 135714 135720 135724 135726 135732 135736 135742 135750 447348
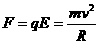 而R=s/θ
而R=s/θ
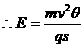
 点评:滑块m向圆弧最低处滑动不同于沿斜面的滑动,这是一个很复杂的变速曲线运动,显然,牛顿定律不能求解,但滑块的运动轨迹是一段圆弧,其运动与受力单摆相同,则只要滑块满足从P点到O点的圆弧对应的圆心角很小,小于10°,则完全可以把滑块的运动等效为“单摆的运动模型”。
点评:滑块m向圆弧最低处滑动不同于沿斜面的滑动,这是一个很复杂的变速曲线运动,显然,牛顿定律不能求解,但滑块的运动轨迹是一段圆弧,其运动与受力单摆相同,则只要滑块满足从P点到O点的圆弧对应的圆心角很小,小于10°,则完全可以把滑块的运动等效为“单摆的运动模型”。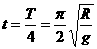
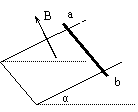 据上述模型分析,导体ab平衡的条件为:
据上述模型分析,导体ab平衡的条件为: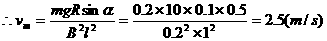

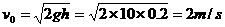
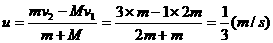
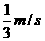 。
。
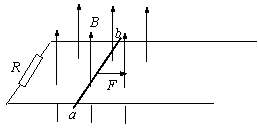 (10分)如图所示,导体棒ab在磁感应强度为B、方向竖直向上的匀强磁场中受水平恒力F作用,以速度v沿光滑导轨匀速向右运动。导轨左端所接电阻为R,导轨自身电阻不计,导体棒电阻为r,导轨间距为L。请你从力F做功与电路中消耗能量的关系证明:导体棒ab中的感应电动势为
(10分)如图所示,导体棒ab在磁感应强度为B、方向竖直向上的匀强磁场中受水平恒力F作用,以速度v沿光滑导轨匀速向右运动。导轨左端所接电阻为R,导轨自身电阻不计,导体棒电阻为r,导轨间距为L。请你从力F做功与电路中消耗能量的关系证明:导体棒ab中的感应电动势为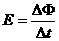 ,并说明其物理意义。
,并说明其物理意义。