广东省中山市2008-2009学年高三第一学期期末统一考试
数学科试卷(理科)
本试卷分第I卷(选择题)、第II卷(非选择题)两部分。共150分,考试时间120分钟。
第Ⅰ卷(选择题 共40分)
注意事项:
1、答第I卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上。
3、不可以使用计算器。
4、考试结束,将答题卡交回,试卷不用上交。
一、选择题(每小题5分,共40分。每小题给出的四个选项中,只有一个选项符合题目要求)
1.函数 是
是
A.周期为 的奇函数 B.周期为
的奇函数 B.周期为 的偶函数
的偶函数
C.周期为 的奇函数 D.周期为
的奇函数 D.周期为 的偶函数
的偶函数
2.已知物体的运动方程为 (t是时间,s是位移),则物体在时刻t=2时的速度为
(t是时间,s是位移),则物体在时刻t=2时的速度为
A. B.
B. C.
C. D.
D.
3.已知 ,那么
,那么
A.-2 B.
4.已知在等差数列{ }中,
}中, 若
若 ,则n的最小值为
,则n的最小值为
A.60 B.62 C.70 D.72
5. 中,若
中,若 ,则
,则 的外接圆半径为
的外接圆半径为
A. B.
B. C.
C. D.
D.
6.若实数 满足条件
满足条件 , 目标函数
, 目标函数 ,则
,则
A. B.
B.
C.  D.
D.
7.底面是矩形的四棱柱 中,
中, ,
, ,
, ,则
,则
A. B.
B. C.
C. D.
D.
8.身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( ) 种。
A.24 B.28 C.36 D.48
第II卷(非选择题共110分)
二、填空题(每小题5分,共30分)
9.若数据 的平均数
的平均数 =5,方差
=5,方差 ,则数据
,则数据
 的平均数为 (2分),方差为 (3分)。
的平均数为 (2分),方差为 (3分)。
10.直线 与抛物线
与抛物线 所围成图形的面积为 .
所围成图形的面积为 .
11.若 ,则
,则 =
.
=
.
12.已知函数 满足,
满足, ,则
,则 =
.
=
.
13.以下有四种说法:
(1)若 为真,
为真, 为假,则
为假,则 与
与 必为一真一假;
必为一真一假;
(2)若数列 的前
的前 项和为
项和为 ,则
,则 ;
;
(3)若 ,则
,则 在
在 处取得极值;
处取得极值;
 (4)由变量x和y的数据得到其回归直线方程
(4)由变量x和y的数据得到其回归直线方程 ,则
,则 一定经过点
一定经过点 .
.
以上四种说法,其中正确说法的序号为 .
14.为迎接校庆,学校准备投入a元建造一个花圃(如图).已知矩形ABCD的造价为40元/ ,其余的两个半圆及两个圆的造价为20元/
,其余的两个半圆及两个圆的造价为20元/ .两圆的直径分别为矩形的长和宽,由于矩形ABCD要种名贵花卉,故建造时要求矩形ABCD的面积越大越好.那么,当矩形ABCD的面积达到最大时,
.两圆的直径分别为矩形的长和宽,由于矩形ABCD要种名贵花卉,故建造时要求矩形ABCD的面积越大越好.那么,当矩形ABCD的面积达到最大时,
三、解答题(共80分.解答题应写出推理、演算步骤)
15. (本题满分12分)
已知向量 ,
,  ,
,
 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,
,  ,
且
,
且 , 求
, 求 .
.
16. (本题满分12分)已知数列 是首项为
是首项为 ,公比
,公比 的等比数列,设
的等比数列,设 ,数列
,数列 .
.
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前n项和Sn.
的前n项和Sn.
17.(本小题满分14分)已知10件产品中有3件是次品.
(I)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(II)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
18. (本题满分14分)如图,四面体ABCD中,O、E分别是BD、BC的中点,


(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦;
(III)求点E到平面ACD的距离.
19. (本题满分14分)已知 ,
, ,
,
 (1)若f(x)在
(1)若f(x)在 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;
(2)如右图所示,若函数 的图象在
的图象在 连续光滑,试猜想拉格朗日中值定理:即一定存在
连续光滑,试猜想拉格朗日中值定理:即一定存在 使得
使得 ?(用含有a,b,f(a),f(b)的表达式直接回答)
?(用含有a,b,f(a),f(b)的表达式直接回答)
(3)利用(2)证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
20. (本题满分14分)已知函数 .
.
(1)若 使
使 ,求实数
,求实数 的取值范围;
的取值范围;
(2)设 ,且
,且 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
中山市高三级2008―2009学年度第一学期期末统一考试
数学科试卷(理科)答案
题号
1
2
3
4
5
6
7
8
答案
B
D
D
B
A
C
C
D
二、填空题(每小题5分,共30分)
9. 16 (2分),18 (3分) 10.  11.
11. 
12.  13. (1) (4) 14.
13. (1) (4) 14. 
三、解答题(共80分.解答题应写出推理、演算步骤)
15. (本题满分12分)
已知向量 ,
,  ,
,
 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,
,  ,
且
,
且 , 求
, 求 .
.
解:(Ⅰ) ,
,  ,
,
 . ……………2分
. ……………2分
 ,
,
 ,
………3分
,
………3分
即
 ,
………5分
,
………5分  .
……………6分
.
……………6分
(Ⅱ) ,
……………7分
,
……………7分
 ,
, 
 ,
,  ……………9分
……………9分 
 .
……………12分
.
……………12分
16. (本题满分12分)已知数列 是首项为
是首项为 ,公比
,公比 的等比数列,,
的等比数列,,
设 ,数列
,数列 .
.
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前n项和Sn.
的前n项和Sn.
解(1)由题意知, ,……………2分
,……………2分
又 ,
,
故  ……………4分
……………4分
(2)由(1)知,
 ……………6分
……………6分
 ……7分
……7分
于是
…………………………9分
两式相减,得


…………………………12分
 ……………12分
……………12分
17.(本小题满分14分)已知10件产品中有3件是次品.
(I)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(II)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
解:(1)任意取出3件产品作检验,全部是正品的概率为 …………3分
…………3分
故至少有一件是次品的概率为1-7/24=17/24……………………6分
(2)设抽取n件产品作检验,则3件次品全部检验出的概率为 ………8分
………8分
由 ……………9分
……………9分
整理得: ,……………………11分
,……………………11分
 ∴当n=9或n=10时上式成立.…………13分
∴当n=9或n=10时上式成立.…………13分
答:任意取出3件产品作检验,其中至少有1件是次品的概率为17/24,为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验.………………14分
 18. (本题满分14分)如图,四面体ABCD中,O、E分别是BD、BC的中点,
18. (本题满分14分)如图,四面体ABCD中,O、E分别是BD、BC的中点,

(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦;
(III)求点E到平面ACD的距离.
解:方法一:
(I)证明:连结OC
 ………1分
………1分

 在
在 中,由已知可得
中,由已知可得
而

 即
即 ……………3分
……………3分
又
 平面
平面 ……………5分
……………5分
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知
 直线OE与EM所成的锐角就是异面直线AB与CD所成的角。……………6分
直线OE与EM所成的锐角就是异面直线AB与CD所成的角。……………6分
在 中,
中,
 ……………7分
……………7分
 是直角
是直角 斜边AC上的中线,
斜边AC上的中线,
 ……………8分
……………8分

 异面直线AB与CD所成角大小的余弦为
异面直线AB与CD所成角大小的余弦为 ;……………9分
;……………9分
(III)解:设点E到平面ACD的距离为
 ……………11分
……………11分
在 中,
中,
 ……………12分
……………12分
而 ……………13分
……………13分

 点E到平面ACD的距离为
点E到平面ACD的距离为 ……………14分
……………14分
方法二:
(II)解:以O为原点,如图建立空间直角坐标系,
(I)同方法一.……………5分
 则
则
 ………………6分
………………6分
 …………7分
…………7分
 ………9分
………9分
 异面直线AB与CD所成角大小的余弦为
异面直线AB与CD所成角大小的余弦为 ;……………10分
;……………10分
(III)解:设平面ACD的法向量为 则
则
 ……………11分
……………11分

令 得
得 是平面ACD的一个法向量.……………12分
是平面ACD的一个法向量.……………12分
又
 点E到平面ACD的距离
点E到平面ACD的距离
 ……………14分
……………14分
19. (本题满分14分)已知 ,
, ,
,
(1)若f(x)在 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;
 (2)如右图所示,若函数
(2)如右图所示,若函数 的图象在
的图象在 连续光滑,试猜想拉格朗日中值定理:即一定存在
连续光滑,试猜想拉格朗日中值定理:即一定存在 使得
使得 ?(用含有a,b,f(a),f(b)的表达式直接回答)
?(用含有a,b,f(a),f(b)的表达式直接回答)
(3)利用(2)证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
解:(1) ,………1分
,………1分
依题意,有 ,即
,即  .……………2分
.……………2分
 ,
, .
.
令 得
得 ,……………4分
,……………4分
从而f(x)的单调增区间为: ;……………5分
;……………5分
(2) ;……………8分
;……………8分
(3)
 ,…………9分
,…………9分

 ……………10分
……………10分

 ………12分
………12分
由(2)知,对于函数y=g(x)图象上任意两点A、B,在A、B之间一定存在一点 ,使得
,使得 ,又
,又 ,故有
,故有 ,证毕.………14分
,证毕.………14分
20. (本题满分14分)已知函数 .
.
(1)若 使
使 ,求实数
,求实数 的取值范围;
的取值范围;
(2)设 ,且
,且 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
解:(1)由 ,
, ,得
,得 ,
, ,……………1分
,……………1分
所以, ……………3分
……………3分
 ;……………4分
;……………4分
(2)由题设得 ,……………5分
,……………5分
对称轴方程为 ,
, 。……………7分
。……………7分
由于 在
在 上单调递增,则有
上单调递增,则有
(Ⅰ)当 即
即 时,有
时,有

 。……………9分
。……………9分
(Ⅱ)当 即
即 时,
时,
设方程 的根为
的根为 ,
,
① 若 ,则
,则 ,有
,有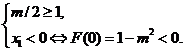
解得 ;……………11分
;……………11分
②若 ,即
,即 ,有
,有 ;
;

 。……………13分
。……………13分
由①②得
 。
。
综合(Ⅰ), (Ⅱ)有  .……………14分
.……………14分