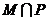江苏省2009届高考数学精编模拟试题(二)
一.填空题
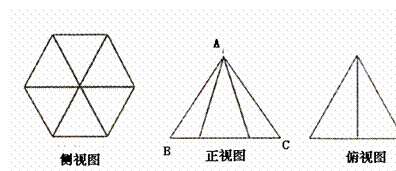
1 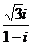 的共轭复数是
的共轭复数是
3.在三棱锥的六条棱中任意选择两条,则这两条棱是一对异面直线的概率
4.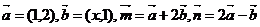 ,且
,且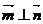 ,则
,则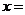
5.函数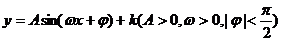 的图象如下,则y的表达式是
的图象如下,则y的表达式是
6.设二次函数 的导数为
的导数为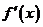 ,
,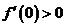 ,对于任意的实数
,对于任意的实数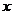 恒有
恒有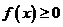 ,则
,则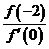 的最小值是
的最小值是
7.在等差数列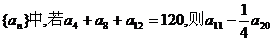 的值是
的值是
8.若直线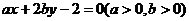 始终平分圆的周
始终平分圆的周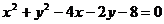 长,则
长,则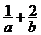 的最小值为
的最小值为
9 .一个总体共有100个个体,随机编号0,1,2,…,99,按从小到大的编号顺序平均分成10个小组,组号依次为1,2,3,…,10,现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=4,则在第6组中抽取的号码是
.一个总体共有100个个体,随机编号0,1,2,…,99,按从小到大的编号顺序平均分成10个小组,组号依次为1,2,3,…,10,现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=4,则在第6组中抽取的号码是
10. 、设球的半径为R, P、Q是球面上北纬600圈上的两点,这两点在纬度圈上的劣弧的长是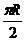 ,则这两点的球面距离是
,则这两点的球面距离是
11. 过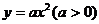 的焦点
的焦点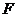 作直线交抛物线与
作直线交抛物线与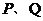 两点,若
两点,若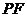 与
与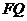 的长分别是
的长分别是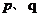 ,则
,则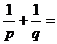
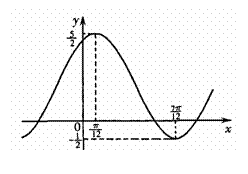
12. 一个几何的三视图如图所示:其中,正视图中△ABC的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为 .
13. 已知0<t<1,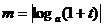 、
、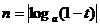 ,则
,则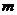 与
与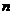 的大小关系为______.
的大小关系为______.
14、不论k为何实数,直线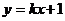 与曲线
与曲线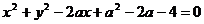 恒有交点,则实数a的取值范围是 。
恒有交点,则实数a的取值范围是 。
二.解答题
15. 已知:复数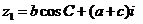 ,
,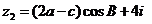 ,且
,且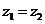 ,其中
,其中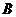 、
、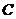 为△ABC的内角,
为△ABC的内角,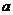 、
、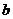 、
、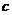 为角
为角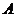 、
、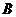 、
、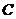 所对的边.
所对的边.
(Ⅰ)求角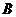 的大小;
的大小;
(Ⅱ) 若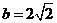 ,求△ABC的面积.
,求△ABC的面积.
16. 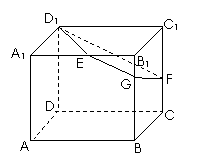 如图,已知正方体
如图,已知正方体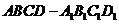 的棱长为2,E、F分别是
的棱长为2,E、F分别是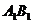 、
、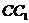 的中点,过
的中点,过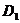 、E、F作平面
、E、F作平面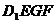 交
交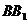 于G..
于G..
(1)求证: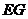 ∥
∥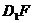 ;
;
(2)求正方体被平面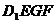 所截得的几何体
所截得的几何体
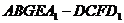 的体积.
的体积.
17.已知圆C: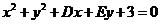 ,圆C关于直线
,圆C关于直线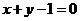 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为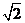
(Ⅰ)求圆C的方程;
(Ⅱ)已知不过原点的直线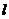 与圆C相切,且在x轴、y轴上的截距相等,求直线
与圆C相切,且在x轴、y轴上的截距相等,求直线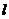 的方程。
的方程。
18. 设实数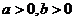 ,且满足
,且满足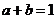
(1)求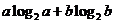 的最小值;
的最小值;
(2)设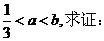 (
(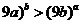
19.已知数列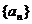 满足:
满足: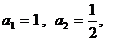 且
且
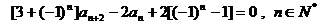 .
.
(Ⅰ)求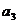 ,
,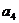 ,
,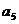 ,
,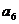 的值及数列
的值及数列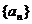 的通项公式;
的通项公式;
(Ⅱ)设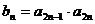 ,求数列
,求数列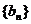 的前
的前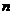 项和
项和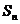 ;
;
20. 已知二次函数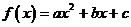 .
.
(1)若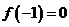 ,试判断函数
,试判断函数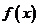 零点个数;
零点个数;
(2)若对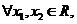 且
且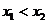 ,
,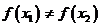 ,试证明
,试证明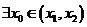 ,使
,使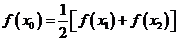 成立。
成立。
(3)是否存在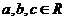 ,使
,使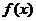 同时满足以下条件①对
同时满足以下条件①对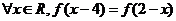 ,且
,且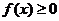 ;②对
;②对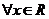 ,都有
,都有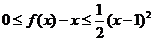 。若存在,求出
。若存在,求出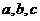 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
试题答案
一.填空题
1. 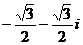 2. 0 3.
2. 0 3. 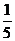 4.
4. 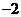 或
或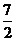 5.
5.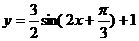
6. 0
7. 30 8.  9. 50 10.
9. 50 10. 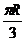
11. 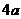 12.
12. 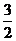 13、
13、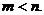 ; 14、
; 14、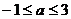 ;
;
二.解答题
15. 解:(Ⅰ)∵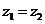 ∴
∴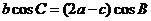 ----①,
----①,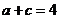 ----②
----②
由①得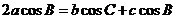 ------③
------③
在△ABC中,由正弦定理得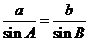 =
=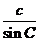 ,设
,设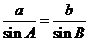
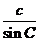 =
=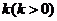
则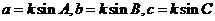 ,代入③得
,代入③得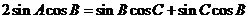
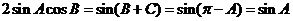
∵ 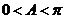 ∴
∴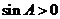 ∴
∴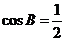 ,∵
,∵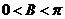 ∴
∴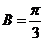
(Ⅱ) ∵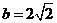 ,由余弦定理得
,由余弦定理得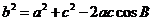
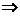
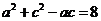 ,--④
,--④
由②得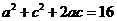 -⑤ 由④⑤得
-⑤ 由④⑤得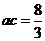 ,∴
,∴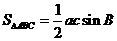 =
=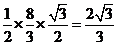 .
.
16. .(1)证明:在正方体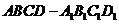 中,∵平面
中,∵平面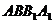 ∥平面
∥平面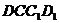
平面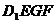
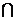 平面
平面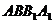
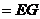 ,平面
,平面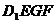
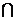 平面
平面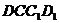
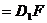
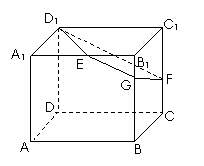 ∴
∴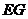 ∥
∥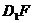 .
.
(2)解:设所求几何体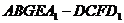 的体积为V,
的体积为V,
∵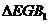 ~
~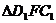 ,
,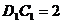 ,
,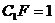 ,
,
∴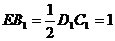 ,
,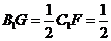 ,
,
∴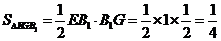 ,
,
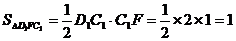
故V棱台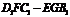
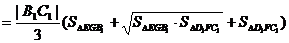
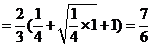
∴V=V正方体-V棱台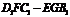
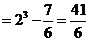 .
.
17. 解:(Ⅰ)由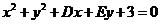 知圆心C的坐标为
知圆心C的坐标为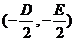
∵圆C关于直线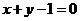 对称
对称
∴点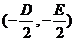 在直线
在直线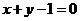 上
上
即D+E=-2,------------①且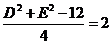 -----------------②
-----------------②
又∵圆心C在第二象限 ∴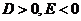
由①②解得D=2,E=-4
∴所求圆C的方程为: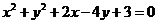
(Ⅱ)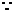 切线在两坐标轴上的截距相等且不为零,设
切线在两坐标轴上的截距相等且不为零,设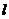 :
: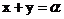
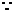 圆C:
圆C: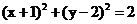
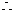 圆心
圆心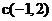 到切线的距离等于半径
到切线的距离等于半径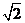 ,
,
即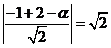
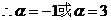 。
。
所求切线方程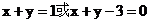
18. .解:(1)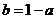 代入得
代入得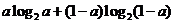
设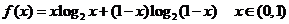
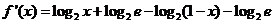
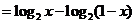 3分
3分
令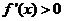 解得
解得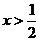
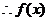 在
在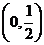 上单调递减,在
上单调递减,在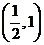 上单调递增。
上单调递增。
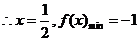 即原式的最小值为-1
即原式的最小值为-1
(2)要证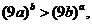 即证
即证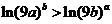
即证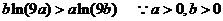
即证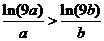
由已知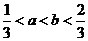 设
设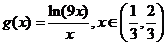
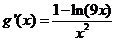
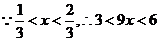
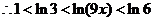
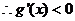
所以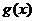 在
在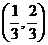 上单调递减,
上单调递减,
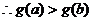
原不等式得证。
19.解:(Ⅰ)经计算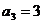 ,
,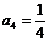 ,
,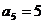 ,
,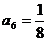 .
.
当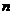 为奇数时,
为奇数时,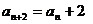 ,即数列
,即数列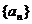 的奇数项成等差数列,
的奇数项成等差数列,
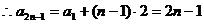 ;
;
当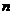 为偶数,
为偶数,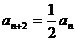 ,即数列
,即数列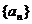 的偶数项成等比数列,
的偶数项成等比数列,
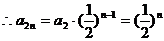 .
.
因此,数列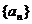 的通项公式为
的通项公式为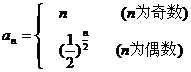 .
.
(Ⅱ)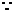
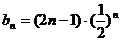 ,
,
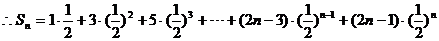 ……(1)
……(1)
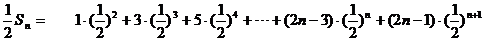 …(2)
…(2)
(1)、(2)两式相减,
得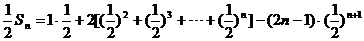
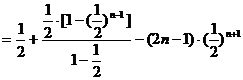
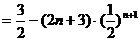 .
.
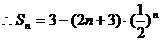 .
.
20. .解(1) 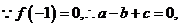
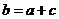
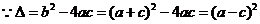 ,
,
当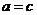 时
时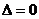 ,函数
,函数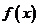 有一个零点;
有一个零点;
当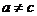 时,
时,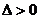 ,函数
,函数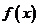 有两个零点。
有两个零点。
(2)令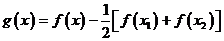 ,则
,则

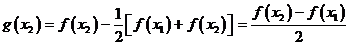 ,
,
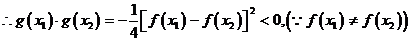
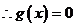 在
在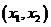 内必有一个实根。即
内必有一个实根。即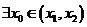 ,使
,使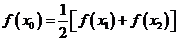 成立。
成立。
(3)
假设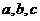 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且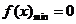
∴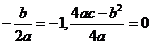
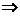
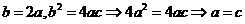
由②知对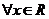 ,都有
,都有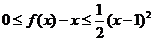
令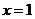 得
得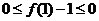
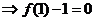
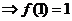
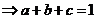
由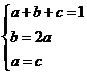 得
得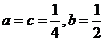 ,
,
当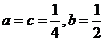 时,
时,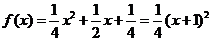 ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又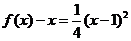
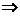 对
对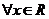 ,都有
,都有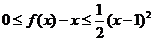 ,满足条件②。
,满足条件②。
∴存在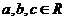 ,使
,使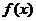 同时满足条件①、②。
同时满足条件①、②。
www.1010jiajiao.com