摘要:(3)是否存在.使同时满足以下条件①对.且,②对,都有.若存在.求出的值.若不存在.请说明理由. 试题答案
网址:http://m.1010jiajiao.com/timu_id_546231[举报]
对定义在![]() 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数![]() 称为
称为![]() 函数.
函数.
① 对任意的![]() ,总有
,总有![]() ;
;
② 当![]() 时,总有
时,总有![]() 成立.
成立.
已知函数![]() 与
与![]() 是定义在
是定义在![]() 上的函数.
上的函数.
(1)试问函数![]() 是否为
是否为![]() 函数?并说明理由;
函数?并说明理由;
(2)若函数![]() 是
是![]() 函数,求实数
函数,求实数![]() 的值;
的值;
(3)在(2)的条件下,是否存在实数![]() ,使方程
,使方程![]() 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知定义域为![]() 的函数
的函数![]() 同时满足以下三个条件:
同时满足以下三个条件:
[1] 对任意的![]() ,总有
,总有![]() ;
;
[2] ![]() ;
;
[3] 若![]() ,
,![]() ,且
,且![]() ,则有
,则有![]() 成立,
成立,
并且称![]() 为“友谊函数”,请解答下列各题:
为“友谊函数”,请解答下列各题:
(1)若已知![]() 为“友谊函数”,求
为“友谊函数”,求![]() 的值;
的值;
(2)函数![]() 在区间
在区间![]() 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知![]() 为“友谊函数”,假定存在
为“友谊函数”,假定存在![]() ,使得
,使得![]() 且
且![]() ,
,
求证:![]() .
.
已知定义域为![]() 的函数
的函数![]() 同时满足以下三个条件:
同时满足以下三个条件:
[1] 对任意的![]() ,总有
,总有![]() ;
;
[2] ![]() ;
;
[3] 若![]() ,
,![]() ,且
,且![]() ,则有
,则有![]() 成立,
成立,
并且称![]() 为“友谊函数”,请解答下列各题:
为“友谊函数”,请解答下列各题:
(1)若已知![]() 为“友谊函数”,求
为“友谊函数”,求![]() 的值;
的值;
(2)函数![]() 在区间
在区间![]() 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知![]() 为“友谊函数”,假定存在
为“友谊函数”,假定存在![]() ,使得
,使得![]() 且
且![]() ,
,
求证:![]() .
.
 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件: ,总有
,总有 ;(2)
;(2) ;(3) 若
;(3) 若 ,
, ,且
,且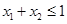 ,则有
,则有 成立,则称
成立,则称 的值;
的值;  在区间
在区间 ,使得
,使得 且
且 , 求证:
, 求证: .
.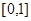 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件: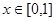 ,总有
,总有 ;
;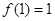 ;
; 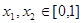 ,且
,且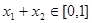 时,
时,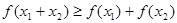 成立.
成立.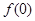 的值;
的值;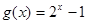 在区间
在区间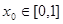 ,使得
,使得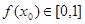 ,且
,且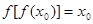 ,求证:
,求证: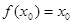 .
.