2009届高三毕业班模拟考试数学(文科)试题

本试卷分选择题和非选择题两部分,共8页,满分为150分。考试用时120分钟。
注意事项:1、答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和学号填写在答题卡和答卷密封线内相应的位置上,用2B铅笔将自己的学号填涂在答题卡上。
2、选择题每小题选出答案后,有2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试卷上。
3、非选择题必须用黑色字迹的钢笔或签字笔在答卷纸上作答,答案必须写在答卷纸各题目指定区域内的相应位置上,超出指定区域的答案无效;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4、考生必须保持答题卡的整洁和平整。
第一部分选择题(共50分)
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中。只有一项是符合题目要求的。
1.若复数 是纯虚数(
是纯虚数(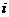 是虚数单位,
是虚数单位, 是实数),则
是实数),则 ( )
( )
A. -2 B.  C.
C. D. 2
D. 2
2.函数 的值域是( )
的值域是( )
A. B.
B. C.
C. D.
D.

3.如图所示,一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的全面积为 ( )
 A.
A.


B.


C.


D.


4.已知函数 定义域是
定义域是 ,则
,则 的定义域是 ( )
的定义域是 ( )
A. B.
B.  C.
C.
 D.
D. 

5.若函数 唯一的一个零点同时在区间
唯一的一个零点同时在区间 、
、 、
、 、
、 内,那么下列命题中正确的是
( )
内,那么下列命题中正确的是
( )
A.函数 在区间
在区间 内有零点 B.函数
内有零点 B.函数 在区间
在区间 或
或 内有零点
内有零点

C.函数 在区间
在区间 内无零点 D.函数
内无零点 D.函数 在区间
在区间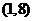 内无零点
内无零点
 6 函数
6 函数 在区间
在区间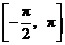 的简图是
( )
的简图是
( )











7. 甲:A1 ,A2是互斥事件;乙:A1 ,A2是对立事件,那么
( )
A 甲是乙的充分但不必要条件 B 甲是乙的必要但不充分条件
C 甲是乙的充要条件 D 甲既不是乙的充分条件,也不是乙的必要条件

8.
直线 与圆
与圆 的位置关系是 ( )
的位置关系是 ( )
A.相离 B.相交 C.相切 D.与 的值有关
的值有关








 9.在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应
9.在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应 收费系统的流程图如图所示,则①处应填( ).
收费系统的流程图如图所示,则①处应填( ).
A B
B


C D
D

10.在双曲线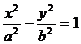 上有一个点P,
上有一个点P,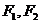 为双曲线两个焦点,
为双曲线两个焦点, ,且
,且 的三条边长成等差数列,则此双曲线得离心率是
( )
的三条边长成等差数列,则此双曲线得离心率是
( )
A.2 B.
第二部分 非选择题(共100分)
二、填空题(本大题共5小题,每小题5分共20分。其中,第14、15两小题是选做题,考生只能选做一题,若两题都做,则只以第14题的得分为最后得分.)

11.设M和m分别表示函数y=2sinx-1的最大值和最小值,则M+m等于
.


12.如图的矩形,长为5,宽为3,在矩形内随机地撒300颗黄豆,
数得落在阴影部分的黄豆数为120颗,则我们可以估计出阴影
部分的面积为
.
13.函数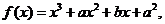 (其中
(其中 )在
)在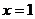 时有极值
时有极值 ,那么
,那么 的值分别为a=
,b=
。
的值分别为a=
,b=
。
14.(坐标系与参数方程选做题)直线 被圆
被圆 所截得的弦长为
.
所截得的弦长为
.
 15.(几何证明选讲选做题)如图所示,圆O的直径AB=10,C为圆周上一点,BC=5,过C作圆的切线
15.(几何证明选讲选做题)如图所示,圆O的直径AB=10,C为圆周上一点,BC=5,过C作圆的切线 ,则点A到直线
,则点A到直线 的距离AD为 .
的距离AD为 .
三.解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知向量 ,且
,且

(Ⅰ)求tanA的值;
(Ⅱ)求函数 R)的值域.
R)的值域.




17.(本小题满分12分)
甲、乙两人各抛掷一次正方体骰子(它们的六个面分别标有数字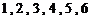 ),设甲、乙所抛掷骰子朝上的面的点数分别为
),设甲、乙所抛掷骰子朝上的面的点数分别为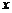 、
、 ,那么
,那么
(I)共有多少种不同的结果?
(II)请列出满足复数 的实部大于虚部的所有结果。
的实部大于虚部的所有结果。
(III)满足复数 的实部大于虚部的概率是多少?
的实部大于虚部的概率是多少?





18.(本小题满分14分)
 如图,在组合体中,
如图,在组合体中,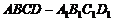 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
, ,点
,点 且
且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)求 与平面
与平面 所成的角的正切值;
所成的角的正切值;
(Ⅲ)若 ,当
,当 为何值时,
为何值时, .
.






19.(本小题满分14分)
已知椭圆C的中心在坐标原点,焦点在y轴上,椭圆上的点到焦点距离的最大值为  ,最小值为
,最小值为 。
。
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线 与C交于A,B两点.若以AB为直径的圆过坐标原点O,求k的值。
与C交于A,B两点.若以AB为直径的圆过坐标原点O,求k的值。
(III)在(Ⅱ)的条件下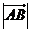 的值是多少?
的值是多少?
20 (本小题满分14分)
已知数列 ,
, 满足
满足 ,
, ,且
,且 (
( )
)
(I)令 ,求数列
,求数列 的通项公式
的通项公式 及前
及前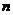 项和公式
项和公式 ;
;
(II)求数列 的通项公式,并由此求
的通项公式,并由此求 和
和 的值以及数列
的值以及数列 的前
的前 项公式
项公式
21.(本小题满分14分)
设函数 (
( ),其中
),其中
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点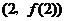 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的极大值和极小值;
的极大值和极小值;
(Ⅲ)当 时,证明存在
时,证明存在 ,使得不等式
,使得不等式 对任意的
对任意的 恒成立
恒成立
2009届高三毕业班模拟考试数学(文科)试题
成绩:
 注意事项:1、本答卷为第二部分非选择题答题区。考生必须用黑色字迹的钢笔或签字笔在各题目指定区域内的相应位置上答题,超出指定区域的答案无效。
注意事项:1、本答卷为第二部分非选择题答题区。考生必须用黑色字迹的钢笔或签字笔在各题目指定区域内的相应位置上答题,超出指定区域的答案无效。
2、如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液,不按以上要求作答的答案无效。

|

 。
。

 ,当
,当 时,
时, 不是极值点
不是极值点 解:把直线
解:把直线 代入
代入
 ,弦长为
,弦长为
 解: C为圆周上一点,AB是直径,所以AC⊥BC,而BC=5,AB=10,∠BAC=30°,从而得∠B=60°,所以∠DCA=60°,又∠ADC=90°,得∠DAC=30°,
解: C为圆周上一点,AB是直径,所以AC⊥BC,而BC=5,AB=10,∠BAC=30°,从而得∠B=60°,所以∠DCA=60°,又∠ADC=90°,得∠DAC=30°,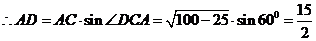
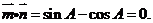 ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 2分
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 2分 ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 5分
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 5分 ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分 ?????????????????????????????????????????????????????????????????????????????????????????????????????????? 7分
?????????????????????????????????????????????????????????????????????????????????????????????????????????? 7分 R,所以
R,所以 .??????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
.??????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 8分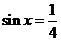 时,f(x)有最大值
时,f(x)有最大值 ,???????????????????????????????????????????????????????????????????????????????????????????????????????? 9分
,???????????????????????????????????????????????????????????????????????????????????????????????????????? 9分 ????????????????????????????????????????????????????????????????????????????????????????????? 12分
????????????????????????????????????????????????????????????????????????????????????????????? 12分
 种结果?????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
种结果?????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分 来表示两枚骰子向上的点数,满足复数
来表示两枚骰子向上的点数,满足复数 ,(3,1),(4,1)(5,1),(6,1)(3,2),(4,2)(5,2),(6,2)(4,3),
,(3,1),(4,1)(5,1),(6,1)(3,2),(4,2)(5,2),(6,2)(4,3), ???????????????????????????????? 12分
???????????????????????????????? 12分 ,所以
,所以 为等腰直角三角形,
为等腰直角三角形, .?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 1分
.?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 1分 ,???????????????????????????????????????????? 2分
,???????????????????????????????????????????? 2分 ,所以
,所以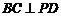 .????????????????????????????????????????????? 3分
.????????????????????????????????????????????? 3分 垂直于平面
垂直于平面 内的两条相交直线
内的两条相交直线 和
和 ,??????????????????????????????????????????????????????? 4分
,??????????????????????????????????????????????????????? 4分 (
( )
) 点在平面
点在平面 作
作 于
于 ,连接
,连接 .??????????????????????????????????????????????? 6分
.??????????????????????????????????????????????? 6分 ,所以
,所以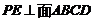 ,????????????????????????????????????????????????????????????????????????? 7分
,????????????????????????????????????????????????????????????????????????? 7分 就是
就是 ,
, ,所以
,所以 .?????????????????????????????????? 9分
.?????????????????????????????????? 9分 .??????????????????????????????????????????????????????????????? 10分
.??????????????????????????????????????????????????????????????? 10分 时,
时, . ???????????????????????????????????????????????????????????????????????????????????? 11分
. ???????????????????????????????????????????????????????????????????????????????????? 11分 ,而
,而 ,
, ,所以
,所以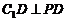 .?????????????????????????????????????????????????????????????????????????????????????????????? 12分
.?????????????????????????????????????????????????????????????????????????????????????????????? 12分 ,
, 与
与 . ??????????????????????????????????????? 13分
. ??????????????????????????????????????? 13分 ,所以
,所以 ,所以
,所以 ????????????????????????????????????????????????????? 1分
????????????????????????????????????????????????????? 1分 ?????????????????????????????????????????????????????????????????????????????????????????????? 2分
?????????????????????????????????????????????????????????????????????????????????????????????? 2分 ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 3分
??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 3分 ???????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
???????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分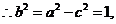 ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 5分
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 5分 .????????????????????????????????????????????????????????????????????????????????????????????? 6分
.????????????????????????????????????????????????????????????????????????????????????????????? 6分 ,其坐标满足
,其坐标满足
 ,???????????????????????????????????????????????????????????????????????????????????????? 7分
,???????????????????????????????????????????????????????????????????????????????????????? 7分 .?????????????????????????????????????????????????????????????????????????????????????????????? 8分
.?????????????????????????????????????????????????????????????????????????????????????????????? 8分 ,即
,即 .???????????????????? 9分
.???????????????????? 9分 ,
, .??????????????????????????????????????????????? 10分
.??????????????????????????????????????????????? 10分 时,
时, ,
, .????????????????????????????????????????????????????????????????????? 12分
.????????????????????????????????????????????????????????????????????? 12分 ,?????????????????????????????????????????????????????????????? 13分
,?????????????????????????????????????????????????????????????? 13分
 ,
, .??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 14分
.??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 14分 ,??????????????????????????????????????????????????????????? 1分
,??????????????????????????????????????????????????????????? 1分 (
( ,公差为2的等差数列,???????????????????????????????????????????????????????????? 3分
,公差为2的等差数列,???????????????????????????????????????????????????????????? 3分 ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分 ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分 ,令
,令 ,则
,则
 是首项为
是首项为 ,公比为
,公比为 ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 8分 ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 9分
??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 9分 ,?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 10分
,?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 10分 ???????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 11分
???????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 11分 ???????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 12分
???????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 12分
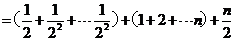 ????????????????????????????????????????????????????????????????????????????????????????? 13分
????????????????????????????????????????????????????????????????????????????????????????? 13分 ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 14分
??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 14分 ,得
,得 ,??????????????????????????????????????????? 1分
,??????????????????????????????????????????? 1分 ,?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 2分
,?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 2分 ????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 3分
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 3分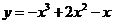 在点
在点 处的切线方程是
处的切线方程是 ,整理得
,整理得 ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
 ,解得
,解得 或
或 ????????????????????????????????????????????????????????????????????????????????????????????????????? 5分
????????????????????????????????????????????????????????????????????????????????????????????????????? 5分 ,当
,当 变化时,
变化时, 的正负如下表:
的正负如下表:






 ,且
,且 ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 7分
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 7分 ,且
,且 ????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 8分 ,当
,当


 ,当
,当 ,
,
 上是减函数,要使
上是减函数,要使
 ①????????????????????????????????????????????????????????????????? 11分
①????????????????????????????????????????????????????????????????? 11分 ,则函数
,则函数 在
在 上的最大值为
上的最大值为 ???? 12分
???? 12分 ,即
,即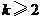 或
或 ???????????????????????????????????????????????????????? 13分
???????????????????????????????????????????????????????? 13分 上存在
上存在 ,使得
,使得