网址:http://m.1010jiajiao.com/timu_id_363011[举报]
在棱长为 的正方体
的正方体 中,
中, 是线段
是线段 的中点,
的中点, .
.
(1) 求证: ^
^ ;
;
(2) 求证: //平面
//平面 ;
;
(3) 求三棱锥 的表面积.
的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中,利用 ,得到结论,第二问中,先判定
,得到结论,第二问中,先判定 为平行四边形,然后
为平行四边形,然后 ,可知结论成立。
,可知结论成立。
第三问中, 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
,
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为 .
.
解: (1)证明:根据正方体的性质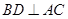 ,
,
因为 ,
,
所以 ,又
,又 ,所以
,所以 ,
, ,
,
所以 ^
^ .
………………4分
.
………………4分
(2)证明:连接 ,因为
,因为 ,
,
所以 为平行四边形,因此
为平行四边形,因此 ,
,
由于 是线段
是线段 的中点,所以
的中点,所以 , …………6分
, …………6分
因为
 面
面 ,
,
 平面
平面 ,所以
,所以 ∥平面
∥平面 . ……………8分
. ……………8分
(3) 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
……………………10分
,
……………………10分
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为

查看习题详情和答案>>
设f (x)=sin 2x+ (sin x-cos x)(sin x+cos x),其中x∈R.
(sin x-cos x)(sin x+cos x),其中x∈R.
(Ⅰ) 该函数的图象可由
 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(Ⅱ)若f (θ)= ,其中
,其中 ,求cos(θ+
,求cos(θ+ )的值;
)的值;
【解析】第一问中,
即 变换分为三步,①把函数
变换分为三步,①把函数 的图象向右平移
的图象向右平移 ,得到函数
,得到函数 的图象;
的图象;
②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的 倍,得到函数
倍,得到函数 的图象;
的图象;
③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数 的图象;
的图象;
第二问中因为 ,所以
,所以 ,则
,则 ,又
,又
 ,
, ,从而
,从而
进而得到结论。
(Ⅰ) 解:
即 。…………………………………3分
。…………………………………3分
变换的步骤是:
①把函数 的图象向右平移
的图象向右平移 ,得到函数
,得到函数 的图象;
的图象;
②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的 倍,得到函数
倍,得到函数 的图象;
的图象;
③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数 的图象;…………………………………3分
的图象;…………………………………3分
(Ⅱ) 解:因为 ,所以
,所以 ,则
,则 ,又
,又
 ,
, ,从而
,从而 ……2分
……2分
(1)当 时,
时, ;…………2分
;…………2分
(2)当 时;
时;
查看习题详情和答案>>
某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表
|
专业 性别 |
非统计专业 |
统计专业 |
|
男 |
13 |
10 |
|
女 |
7 |
20 |
为了判断主修统计专业是否与性别有关系,根据表中的数据,得到
 ,因为
,因为 ,所以判定主修统计专业与性别有关系,这种判断出错的可能性为_________
,所以判定主修统计专业与性别有关系,这种判断出错的可能性为_________
|
|
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
查看习题详情和答案>>
在数学证明中,①假言推理、②三段论推理、③传递关系推理、④完全归纳推理,是经常使用的四种演绎推理,下面推理过程使用到上述推理规则中的( )如(右图)

因为l AB,所以
AB,所以 又因为AB//CD,所以
又因为AB//CD,所以
所以
A. ①②③ B.②③④
C. ②③ D.①②③④
查看习题详情和答案>>
设点 是抛物线
是抛物线

 的焦点,
的焦点, 是抛物线
是抛物线 上的
上的 个不同的点(
个不同的点(
 ).
).
(1) 当 时,试写出抛物线
时,试写出抛物线 上的三个定点
上的三个定点 、
、 、
、 的坐标,从而使得
的坐标,从而使得
 ;
;
(2)当 时,若
时,若 ,
,
求证: ;
;
(3) 当 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即:
“若 ,则
,则 .”
.”
开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
① 试构造一个说明该逆命题确实是假命题的反例(本研究方向最高得4分);
② 对任意给定的大于3的正整数 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
③ 如果补充一个条件后能使该逆命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由(本研究方向最高得10分).
【评分说明】本小题若填空不止一个研究方向,则以实得分最高的一个研究方向的得分作为本小题的最终得分.
【解析】第一问利用抛物线 的焦点为
的焦点为 ,设
,设 ,
,
分别过 作抛物线
作抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 .
.
由抛物线定义得到
第二问设 ,分别过
,分别过 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为 .
.
由抛物线定义得


第三问中①取 时,抛物线
时,抛物线 的焦点为
的焦点为 ,
,
设 ,
, 分别过
分别过
 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为
 .由抛物线定义得
.由抛物线定义得




 ,
,
则 ,不妨取
,不妨取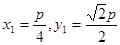 ;
;
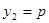 ;
;
 ;
;
解:(1)抛物线 的焦点为
的焦点为 ,设
,设 ,
,
分别过 作抛物线
作抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 .由抛物线定义得
.由抛物线定义得


因为 ,所以
,所以 ,
,
故可取

 满足条件.
满足条件.
(2)设 ,分别过
,分别过 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为 .
.
由抛物线定义得


 又因为
又因为



 ;
;
所以

 .
.
(3) ①取 时,抛物线
时,抛物线 的焦点为
的焦点为 ,
,
设 ,
, 分别过
分别过
 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为
 .由抛物线定义得
.由抛物线定义得




 ,
,
则 ,不妨取
,不妨取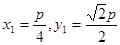 ;
;
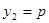 ;
;
 ;
; ,
,
则

 ,
,

 .
.
故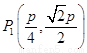 ,
, ,
, ,
, 是一个当
是一个当 时,该逆命题的一个反例.(反例不唯一)
时,该逆命题的一个反例.(反例不唯一)
② 设 ,分别过
,分别过 作
作
抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
,
由 及抛物线的定义得
及抛物线的定义得
 ,即
,即 .
.
因为上述表达式与点 的纵坐标无关,所以只要将这
的纵坐标无关,所以只要将这 点都取在
点都取在 轴的上方,则它们的纵坐标都大于零,则
轴的上方,则它们的纵坐标都大于零,则






 ,
,
而 ,所以
,所以 .
.
(说明:本质上只需构造满足条件且 的一组
的一组 个不同的点,均为反例.)
个不同的点,均为反例.)
③ 补充条件1:“点 的纵坐标
的纵坐标 (
( )满足
)满足  ”,即:
”,即:
“当 时,若
时,若 ,且点
,且点 的纵坐标
的纵坐标 (
( )满足
)满足 ,则
,则 ”.此命题为真.事实上,设
”.此命题为真.事实上,设 ,
,
分别过 作抛物线
作抛物线 准线
准线 的垂线,垂足分别为
的垂线,垂足分别为 ,由
,由 ,
,
及抛物线的定义得 ,即
,即 ,则
,则






 ,
,
又由 ,所以
,所以 ,故命题为真.
,故命题为真.
补充条件2:“点 与点
与点
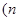 为偶数,
为偶数, 关于
关于 轴对称”,即:
轴对称”,即:
“当 时,若
时,若 ,且点
,且点 与点
与点
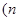 为偶数,
为偶数, 关于
关于 轴对称,则
轴对称,则 ”.此命题为真.(证略)
”.此命题为真.(证略)
查看习题详情和答案>>

