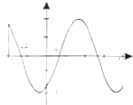
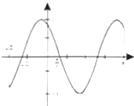
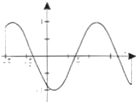
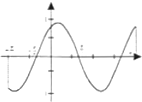
摘要：6 函数在区间的简图是 ( )
网址：http://m.1010jiajiao.com/timu_id_362891[举报]
已知奇函数f（x）=cos（ωx+φ）（ω＞0，且-π≤φ≤0）的定义域为R，其图象C关于直线x=
对称，又f（x）在区间[0，
]上是单调函数．
（1）求函数f（x）的表达式；
（2）将图象C向右平移
个单位后，得到函数y=g（x）的图象．
①化简，并求值：
+4f（10°）；
②若关于x的方程f（x）=g（x）+m在区间[0，
]上有唯一实根，求实数m的取值范围．
查看习题详情和答案>>
| π |
| 4 |
| π |
| 6 |
（1）求函数f（x）的表达式；
（2）将图象C向右平移
| π |
| 4 |
①化简，并求值：
| 1+f(20°)+g(20°) |
| 1+f(20°)-g(20°) |
②若关于x的方程f（x）=g（x）+m在区间[0，
| π |
| 6 |
已知奇函数f（x）=cos（ωx+φ）（ω＞0，且-π≤φ≤0）的定义域为R，其图象C关于直线x=
对称，又f（x）在区间[0，
]上是单调函数．
（1）求函数f（x）的表达式；
（2）将图象C向右平移
个单位后，得到函数y=g（x）的图象．
①化简，并求值：
+4f（10°）；
②若关于x的方程f（x）=g（x）+m在区间[0，
]上有唯一实根，求实数m的取值范围．
查看习题详情和答案>>
| π |
| 4 |
| π |
| 6 |
（1）求函数f（x）的表达式；
（2）将图象C向右平移
| π |
| 4 |
①化简，并求值：
| 1+f(20°)+g(20°) |
| 1+f(20°)-g(20°) |
②若关于x的方程f（x）=g（x）+m在区间[0，
| π |
| 6 |
“你低碳了吗？”这是某市为倡导建设
节约型社会而发布的公益广告里的一句话．
活动组织者为了了解这则广告的宣传效果，
随机抽取了120名年龄在[10，20) ，[20，30) ，
…， [50，60) 的市民进行问卷调查，由此
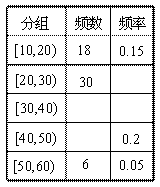得到的样本的频率分布直方图如图所示．
(1) 根据直方图填写右面频率分布统计表；
(2) 按分层抽样的方法在受访市民中抽取
名市民作为本次活动的获奖者，
若在[10，20)的年龄组中随机抽取了6人，
则的值为多少？
(3) 根据直方图，试估计受访市民年龄的
中位数（保留整数）；
19（9分）已知函数
,
(1) 用“五点法”作出在一个周期内
的简图.（列表、作图）
(2) 写出的对称轴方程、对称中心及单调递减区间.
(3) 函数y=sinx的图象经过怎样的变换可得到的图象.