【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
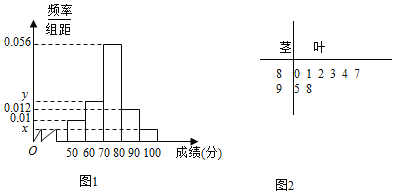
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
【题目】某企业对设备进行升级改造,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测一项质量指标值,若该项指标值落在[20,40)内的产品视为合格品,否则为不合格品,图1是设备改造前样本的频率分布直方图,表1是设备改造后的频数分布表.

表1,设备改造后样本的频数分布表:
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)请估计该企业在设备改造前的产品质量指标的平均数;
(2)企业将不合格品全部销毁后,并对合格品进行等级细分,质量指标值落在[25,30)内的定为一等品,每件售价240元,质量指标值落在[20,25)或[30,35)内的定为二等品,每件售价180元,其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率,现有一名顾客随机购买两件产品,设其支付的费用为X(单位:元),求X得分布列和数学期望.
【题目】为了了解![]() 地区足球特色学校的发展状况,某调查机构得到如下统计数据:
地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(2)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测
,并预测![]() 地区2019年足球特色学校的个数(精确到个).
地区2019年足球特色学校的个数(精确到个).
本题参考公式和数据: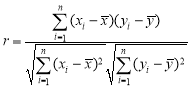 ,
,![]() ,
,![]() ,
,![]() ,
,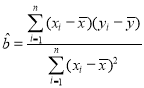 ,
,![]() .
.
【题目】下面给出三个游戏,袋子中分别装有若干只有颜色不同的小球(大小,形状,质量等均一样),从袋中无放回地取球,则其中不公平的游戏是______.
游戏1 | 游戏2 | 游戏3 | |
球数 | 3个黑球和一个白球 | 一个黑球和一个白球 | 2个黑球和2个白球 |
取法 | 取1个球,再取1个球 | 取1个球 | 取1个球,再取1个球 |
胜利 规则 | 取出的两个球同色→甲胜 | 取出的球是黑球→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 |