题目内容
【题目】某会议共出席
个人
，其中每两个人都恰好同其余
个人相互问候过，对任何两个人，同这两个人都问候过的人数是相同的.问共有多少人出席会议?
【答案】36
【解析】
将人视为点，相识连线，毎点共组成
个角，毎个角恰对应一个顶点，因此图中共有角
个.另一方面，设毎两个人，与该二人都相识的人有n个，因此对该二人对张n个角，毎角对应惟一一个二人，对毎二人对张且仅张有n个角， 从这一角度说总角数为
.
当然有
，整理得
，其中n，k均为整数.易见
，没n=3m，进一步化简得
，即
.当
时，
，
不可能为整数.对于
，
只有当k=3时，
取整数，因此只可能是36人.
下面构造一个实例说明命题的情况存在.
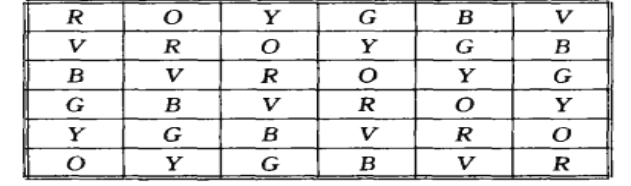
如表R、O、Y、G、B、V表示6种颜色，将人染色，按上图排布，毎人恰好认识与他坐在同一行或同一列或与他具有相同顏色的人.这样，保证了毎人恰认识15个人，只需再证这种构造满足第二个条件即可.
设P、Q是任二个与会者，若他们坐在同一行，则与这两人都认识的人有这一行的其余4个人以及位于P所在列与Q同色的人，和位于Q所在列与P同色的人.当P、Q同色或位于同列均可类似地分析.假定P和Q不同行，不同列，且具有不同的颜色，则二人共同认识的6个人分别是:位于P所在的行和Q所在的列的1个人(与P、Q均不同色)，位于p所在列和Q所在行的1个人，位于p所在行和列且与Q同色的2个人，位于Q所在行和列且与p同色的2个人.
【题目】下面给出三个游戏，袋子中分别装有若干只有颜色不同的小球（大小，形状，质量等均一样），从袋中无放回地取球，则其中不公平的游戏是______.
游戏1 | 游戏2 | 游戏3 | |
球数 | 3个黑球和一个白球 | 一个黑球和一个白球 | 2个黑球和2个白球 |
取法 | 取1个球，再取1个球 | 取1个球 | 取1个球，再取1个球 |
胜利 规则 | 取出的两个球同色→甲胜 | 取出的球是黑球→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 |
