题目内容
【题目】对于区间[a,b](a<b),若函数![]() 同时满足:①
同时满足:①![]() 在[a,b]上是单调函数,②函数
在[a,b]上是单调函数,②函数![]() 在[a,b]的值域是[a,b],则称区间[a,b]为函数
在[a,b]的值域是[a,b],则称区间[a,b]为函数![]() 的“保值”区间
的“保值”区间
(1)求函数![]() 的所有“保值”区间
的所有“保值”区间
(2)函数![]() 是否存在“保值”区间?若存在,求
是否存在“保值”区间?若存在,求![]() 的取值范围,若不存在,说明理由
的取值范围,若不存在,说明理由
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由已知中的保值区间的定义,结合函数![]() 的值域是
的值域是![]() ,可得
,可得![]() ,从而函数
,从而函数![]() 在区间
在区间![]() 上单调,列出方程组,可求解;
上单调,列出方程组,可求解;
(2)根据已知保值区间的定义,分函数![]() 在区间
在区间![]() 上单调递减和函数
上单调递减和函数![]() 在区间
在区间![]() 单调递增,两种情况分类讨论,即可得到答案.
单调递增,两种情况分类讨论,即可得到答案.
(1)因为函数![]() 的值域是
的值域是![]() ,且
,且![]() 在
在![]() 的最后综合讨论结果,
的最后综合讨论结果,
即可得到值域是![]() ,所以
,所以![]() ,所以
,所以![]() ,从而函数
,从而函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
故有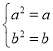 ,解得
,解得 .
.
又![]() ,所以
,所以![]() .所以函数
.所以函数![]() 的“保值”区间为
的“保值”区间为![]() .
.
(2)若函数![]() 存在“保值”区间,则有:
存在“保值”区间,则有:
①若![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以 ,消去
,消去![]() 得
得![]() ,整理得
,整理得![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() .又
.又![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
②若![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以 ,消去
,消去![]() 得
得![]() ,整理得
,整理得![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
综合①、②得,函数![]() 存在“保值”区间,此时
存在“保值”区间,此时![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】探究函数![]() ,x∈(0,+∞)取最小值时x的值,列表如下:
,x∈(0,+∞)取最小值时x的值,列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成以下的问题:
(1)函数![]() (x>0)在区间(0,2)上递减;函数
(x>0)在区间(0,2)上递减;函数![]() 在区间________上递增.当x=_________时,
在区间________上递增.当x=_________时,![]() _______.
_______.
(2)证明:函数![]() (x>0)在区间(O,2)上递减.
(x>0)在区间(O,2)上递减.