题目内容
【题目】某企业对设备进行升级改造,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测一项质量指标值,若该项指标值落在[20,40)内的产品视为合格品,否则为不合格品,图1是设备改造前样本的频率分布直方图,表1是设备改造后的频数分布表.

表1,设备改造后样本的频数分布表:
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)请估计该企业在设备改造前的产品质量指标的平均数;
(2)企业将不合格品全部销毁后,并对合格品进行等级细分,质量指标值落在[25,30)内的定为一等品,每件售价240元,质量指标值落在[20,25)或[30,35)内的定为二等品,每件售价180元,其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率,现有一名顾客随机购买两件产品,设其支付的费用为X(单位:元),求X得分布列和数学期望.
【答案】(1) 30.2;(2)分布列见解析, 400.
【解析】
(1)每个矩形的中点横坐标与该矩形的纵坐标、组距相乘后求和可得平均值;(2)![]() 的可能取值为:240, 300,360, 420, 480,根据直方图求出样本中一、二、三等品的频率分别为
的可能取值为:240, 300,360, 420, 480,根据直方图求出样本中一、二、三等品的频率分别为![]() ,利用独立事件与互斥事件概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得
,利用独立事件与互斥事件概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得![]() 的数学期望.
的数学期望.
(1)样本的质量指标平均值为![]()
![]() .
.
根据样本质量指标平均值估计总体质量指标平均值为30.2 .
(2)根据样本频率分布估计总体分布,样本中一、二、三等品的频率分别为![]() ,
,
故从所有产品中随机抽一件,是一、二、三等品的概率分别为![]() ,
,
随机变量![]() 的取值为:240, 300,360, 420, 480,
的取值为:240, 300,360, 420, 480,
![]() ;
;![]() ,
,
![]() ,
,
所以随机变量![]() 的分布列为:
的分布列为:
| 240 | 300 | 360 | 420 | 480 |
|
|
|
|
|
|
![]() .
.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案【题目】已知函数y=a+bx与![]() ,若对于任意一点
,若对于任意一点![]() ,过点
,过点![]() 作与X轴垂直的直线,交函数y=a+bx的图象于点
作与X轴垂直的直线,交函数y=a+bx的图象于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() ,定义:
,定义:![]() ,若
,若![]() 则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数
则用函数y=a+bx来拟合Y与X之间的关系更合适,否则用函数![]() 来拟合Y与X之间的关系
来拟合Y与X之间的关系
(1)给定一组变量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),对于函数![]() 与函数
与函数![]() ,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
,试利用定义求Q1,Q2的值,并判断哪一个更适合作为点PI(xi,yi)(i=1,2,3…6)中的Y与X之间的拟合函数;
(2)若一组变量的散点图符合![]() 图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当
图象,试利用下表中的有关数据与公式求y对x的回归方程, 并预测当![]() 时,
时,![]() 的值为多少.
的值为多少.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中的![]()
(附:对于一组数据![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为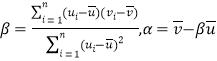 )
)
