15．
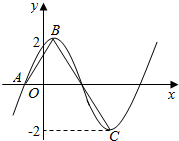已知函数$f（x）=2sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示，A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点．若f（0）=$\sqrt{3}$，
且$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8．则f（x）的解析式为（ ）
已知函数$f（x）=2sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示，A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点．若f（0）=$\sqrt{3}$，且$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8．则f（x）的解析式为（ ）
| A． | f（x）=2sin（2x+$\frac{π}{3}$） | B． | f（x）=2sin（2x+$\frac{π}{6}$） | C． | f（x）=2sin（3x+$\frac{π}{3}$） | D． | f（x）=2sin（3x+$\frac{π}{6}$） |
14．关于平面向量$\overrightarrow a，\overrightarrow b，\overrightarrow c$．下列判断中正确的是（ ）
| A． | 若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$，则$\overrightarrow b=\overrightarrow c$ | B． | 若$\overrightarrow a=（1，k）$，$\overrightarrow b=（-2，6）$，$\overrightarrow a∥$$\overrightarrow b$，则k=$\frac{1}{3}$ | ||
| C． | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|，则$\overrightarrow a•\overrightarrow b=0$ | D． | 若$\overrightarrow a$与$\overrightarrow b$是单位向量，则$\overrightarrow a•\overrightarrow b=1$． |
13．如果cosα=$\frac{4}{5}$，那么$sin（α+\frac{π}{4}）-\frac{{\sqrt{2}}}{2}$cosα等于（ ）
| A． | $\frac{{2\sqrt{2}}}{5}$ | B． | ±$\frac{{2\sqrt{2}}}{5}$ | C． | $\frac{{3\sqrt{2}}}{10}$ | D． | ±$\frac{{3\sqrt{2}}}{10}$ |
12．把函数y=sinx的图象上所有点向右平移$\frac{π}{3}$个单位，再将图象上所有点的横坐标缩小到原来的$\frac{1}{2}$（纵坐标不变），所得函数解析式为y=sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜0），则（ ）
0 247357 247365 247371 247375 247381 247383 247387 247393 247395 247401 247407 247411 247413 247417 247423 247425 247431 247435 247437 247441 247443 247447 247449 247451 247452 247453 247455 247456 247457 247459 247461 247465 247467 247471 247473 247477 247483 247485 247491 247495 247497 247501 247507 247513 247515 247521 247525 247527 247533 247537 247543 247551 266669
| A． | ω=2，φ=-$\frac{π}{3}$ | B． | ω=2，φ=-$\frac{π}{6}$ | C． | ω=$\frac{1}{2}，φ=-\frac{π}{6}$ | D． | ω=$\frac{1}{2}，φ=-\frac{π}{3}$ |
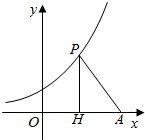如图，已知A（10，0），直线x=t（0＜t＜10）与函数y=ex的图象交于点P，与x轴交于点H，记△APH的面积为f（t）．