题目内容
9.已知函数f(x)=ax2+$\frac{1}{x}$,其中a为常数(1)根据a的不同取值,判断函数f(x)的奇偶性,并说明理由;
(2)若h(x)=f(x)-x-$\frac{1}{x}$>0在[1,2]上恒成立,求a的取值范围.
分析 (1)求出函数的定义域,求得f(-x),对a讨论,当a=0时,当a≠0时,由奇偶性的定义,即可判断;
(2)运用参数分离,求得右边函数的最大值,由恒成立思想,即可得到a的范围.
解答 解:(1)f(x)的定义域为{x|x≠0,x∈R},关于原点对称,
$f(-x)=a{(-x)^2}+\frac{1}{-x}=a{x^2}-\frac{1}{x}$,
当a=0时,f(-x)=-f(x)为奇函数;
当a≠0时,由f(1)=a+1,f(-1)=a-1,
知f(-1)≠-f(1),
故f(x)即不是奇函数也不是偶函数.
(2)由题意可得h(x)=ax2-x>0在[1,2]上恒成立,
即a>($\frac{1}{x}$)max,
由y=$\frac{1}{x}$在[1,2]递减,可得($\frac{1}{x}$)max=1,
即有a>1.
点评 本题考查函数的奇偶性的判断,注意运用定义和分类讨论的思想方法,同时考查不等式恒成立思想转化为求函数的最值问题,属于中档题.

练习册系列答案
相关题目
19.用样本频率分布估计总体频率分布的过程中,下列说法正确的是( )
| A. | 总体容量越大,估计越精确 | B. | 总体容量越小,估计越精确 | ||
| C. | 样本容量越大,估计越精确 | D. | 样本容量越小,估计越精确 |
14.关于平面向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$.下列判断中正确的是( )
| A. | 若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$,则$\overrightarrow b=\overrightarrow c$ | B. | 若$\overrightarrow a=(1,k)$,$\overrightarrow b=(-2,6)$,$\overrightarrow a∥$$\overrightarrow b$,则k=$\frac{1}{3}$ | ||
| C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow a•\overrightarrow b=0$ | D. | 若$\overrightarrow a$与$\overrightarrow b$是单位向量,则$\overrightarrow a•\overrightarrow b=1$. |
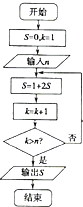 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S=15,那么n的值为( )
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S=15,那么n的值为( )