题目内容
17.计算$cos(\frac{π}{2}+\frac{π}{3})+sin(-π-\frac{π}{6})$的值-$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$.分析 原式利用诱导公式化简,再利用特殊角的三角函数值计算即可得到结果.
解答 解:原式=-sin$\frac{π}{3}$+sin$\frac{π}{6}$=-$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$.
故答案为:-$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$
点评 此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
7.不等式$\frac{2-x}{x-4}≤0$的解集为( )
| A. | {x|-2≤x<4} | B. | {x|x≤2} | C. | {x|x>-4} | D. | {x|x≤2或x>4} |
8.阅读如图的程序框图.若输入n=1,则输出k的值为( )
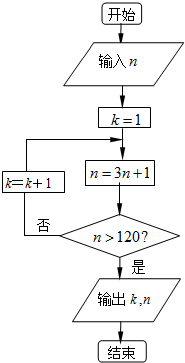

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
12.把函数y=sinx的图象上所有点向右平移$\frac{π}{3}$个单位,再将图象上所有点的横坐标缩小到原来的$\frac{1}{2}$(纵坐标不变),所得函数解析式为y=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<0),则( )
| A. | ω=2,φ=-$\frac{π}{3}$ | B. | ω=2,φ=-$\frac{π}{6}$ | C. | ω=$\frac{1}{2},φ=-\frac{π}{6}$ | D. | ω=$\frac{1}{2},φ=-\frac{π}{3}$ |