题目内容
14.关于平面向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$.下列判断中正确的是( )| A. | 若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$,则$\overrightarrow b=\overrightarrow c$ | B. | 若$\overrightarrow a=(1,k)$,$\overrightarrow b=(-2,6)$,$\overrightarrow a∥$$\overrightarrow b$,则k=$\frac{1}{3}$ | ||
| C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow a•\overrightarrow b=0$ | D. | 若$\overrightarrow a$与$\overrightarrow b$是单位向量,则$\overrightarrow a•\overrightarrow b=1$. |
分析 利用向量的相关知识对选项分别分析选择.
解答 解:对于A,若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$,则$\overrightarrow{a}•(\overrightarrow{b}-\overrightarrow{c})$=0,则$\overrightarrow b=\overrightarrow c$或者$\overrightarrow{a}=\overrightarrow{0}$或者$\overrightarrow{b}-\overrightarrow{c}$垂直$\overrightarrow{a}$;故A错误;
对于B,若$\overrightarrow a=(1,k)$,$\overrightarrow b=(-2,6)$,$\overrightarrow a∥$$\overrightarrow b$,则-2k=6,所以k=$-\frac{1}{3}$;故B 错误;
对于C,|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,两边平方,化简得到$\overrightarrow a•\overrightarrow b=0$;故C正确;
对于D,若$\overrightarrow a$与$\overrightarrow b$是单位向量,则$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cosθ$=cosθ,θ为两个向量的夹角,所以$\overrightarrow a•\overrightarrow b=1$错误.
故选:C.
点评 本题考查了向量的数量积公式,向量平行的坐标关系等;熟练掌握向量的经常知识是关键,属于基础题.

 阅读快车系列答案
阅读快车系列答案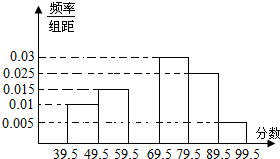 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下,回答下列问题:| 分组 | 人数 | 频率 |
| [39.5,49.5) | a | 0.10 |
| [49.5,59.5) | 9 | x |
| [59.5,69.5) | b | 0.15 |
| [69.5,79.5) | 18 | 0.30 |
| [79.5,89.5) | 15 | y |
| [89.5,99.5] | 3 | 0.05 |
(2)估计这次环保知识竞赛平均分;
(3)若从所有参加环保知识竞赛的学生中随机抽取一人采访,抽到的学生成绩及格的概率有多大?
| A. | $x=\frac{5π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{12}$ | D. | x=-$\frac{π}{12}$ |
| A. | 向左平移1个单位 | B. | 向右平移1个单位 | C. | 向左平移3个单位 | D. | 向右平移3个单位 |