��Ŀ����
10��2015��10��18�����˻ῪĻ��Ϊ�˸��õ�ӭ�����˻ᣬ�����ļ����µ�ͬʱҪ������Դ��ģ������к�Ͽ�������ĵ���������ǽ��Ҫ������Ȳ㣮������Ҫ�����ʹ��30��ĸ��Ȳ㣬ÿ����ĸ��Ȳ㽨��ɱ�Ϊ2��Ԫ���ý�����ÿ�����Դ���ķ���C��Ԫ����Ȳ���xcm�����ϵ��C��x��=$\frac{k}{x+5}$��0��x��10��kΪ�����������������Ȳ㣬ÿ����Դ���ķ���Ϊ3��Ԫ����f��x��Ϊ���Ȳ㽨�������30�����Դ���ķ���֮�ͣ���1����k��ֵ��f��x���ı���ʽ��
��2�����Ȳ������ʱ���ܷ���f��x���ﵽ��С��������Сֵ��
���� ��1���ɸý�����ÿ�����Դ���ķ���C��Ԫ����Ȳ���xcm�����ϵ��C��x��=$\frac{k}{x+5}$��0��x��10��kΪ�����������������Ȳ㣬ÿ����Դ���ķ���Ϊ3��Ԫ�����ǿɵ�C��0��=3����k=15�������õ�f��x���ı���ʽ��
��2���ɣ�1���������f��x���ı���ʽ���������û�������ʽ����ܷ���f��x������Сֵ��
��� �⣺��1����x=0ʱ��c=3����k=15������2�֣���$C��x��=\frac{15}{x+5}$����3�֣�
��$f��x��=2x+\frac{30��15}{x+5}=2x+\frac{450}{x+5}��{0��x��10}��$����6�֣���������ûд��1�֣�
��2��f��x��=2��x+5��+$\frac{450}{x+5}$-10��50��
���ҽ���2��x+5��=$\frac{450}{x+5}$����x=10ʱ��ȡ�Ⱥţ�
��x=10ʱf��x������СֵΪ50����11�֣�
�𣺸��Ȳ���10cm��ʱ���ܷ���f��x���ﵽ��С����СֵΪ50��Ԫ������12�֣�
���� ������ʵ��Ӧ���⣬����Ҫ�����������ģ����ģ����ԭ�ĸ����̣��ڽ�ģʱҪע��ʵ��������Ա���xȡֵ��Χ�����ƣ���ģʱҲҪʵ������ʵ�ʿ��ǣ���ʵ�ʵ����С�������⣬���ú���ģ�ͣ�ת��Ϊ���������С�������Ż������У������˼·֮һ��

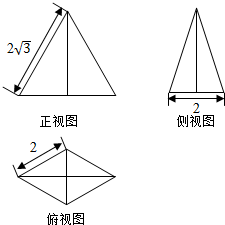 ��ͼ��ij�����������ͼ������ͼ��������ͼ������ͼ������ͼ�ֱ��DZ߳�Ϊ2$\sqrt{3}$�ĵȱ������Σ��ױ߳�Ϊ2�ĵ��������κ����Σ���ü��������Ϊ��������
��ͼ��ij�����������ͼ������ͼ��������ͼ������ͼ������ͼ�ֱ��DZ߳�Ϊ2$\sqrt{3}$�ĵȱ������Σ��ױ߳�Ϊ2�ĵ��������κ����Σ���ü��������Ϊ��������| A�� | 2$\sqrt{3}$ | B�� | 4 | C�� | 4$\sqrt{3}$ | D�� | 2 |
| A�� | $��{-\frac{1}{2}��\frac{1}{2}}]$ | B�� | $��{-\frac{1}{2}��\frac{1}{2}}��$ | C�� | $��{-�ޣ�-\frac{1}{2}}��$ | D�� | $[{\frac{1}{2}��+��}��$ |
| A�� | B⊆A | B�� | A⊆B | C�� | A=B | D�� | A��B=�� |
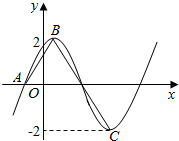 ��֪����$f��x��=2sin����x+�գ����أ�0��|��|��\frac{��}{2}��$�IJ���ͼ����ͼ��ʾ��A��B��C�ֱ��Ǻ���ͼ����x�ύ�㡢ͼ�����ߵ㡢ͼ�����͵㣮��f��0��=$\sqrt{3}$��
��֪����$f��x��=2sin����x+�գ����أ�0��|��|��\frac{��}{2}��$�IJ���ͼ����ͼ��ʾ��A��B��C�ֱ��Ǻ���ͼ����x�ύ�㡢ͼ�����ߵ㡢ͼ�����͵㣮��f��0��=$\sqrt{3}$����$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{��}^{2}}{8}$-8����f��x���Ľ���ʽΪ��������
| A�� | f��x��=2sin��2x+$\frac{��}{3}$�� | B�� | f��x��=2sin��2x+$\frac{��}{6}$�� | C�� | f��x��=2sin��3x+$\frac{��}{3}$�� | D�� | f��x��=2sin��3x+$\frac{��}{6}$�� |
| A�� | $\frac{\sqrt{3}}{3}$ | B�� | 1 | C�� | $\sqrt{3}$ | D�� | $\frac{\sqrt{2}}{2}$ |