题目内容
18．已知△ABC的三个顶点的直角坐标分别为A（2，-1），B（0，0），C（2+m，-2），且∠BAC为钝角，则实数m的取值范围为（-$\frac{1}{2}$，2）∪（2，+∞）．分析 由已知可求$\overrightarrow{AB}$，$\overrightarrow{AC}$的坐标，又∠BAC是钝角，则向量$\overrightarrow{AB}$•$\overrightarrow{AC}$＜0，化简即可．
解答 解：由题意知：$\overrightarrow{AB}$=（-2，1），$\overrightarrow{AC}$=（m，-1），又∠BAC是钝角，所以$\overrightarrow{AB}$•$\overrightarrow{AC}$＜0，
即-2m-1＜0
∴m＞-$\frac{1}{2}$且m≠2．
故答案为：（-$\frac{1}{2}$，2）∪（2，+∞）．
点评 本题主要考查了坐标和向量的对应关系，考查了余弦定理的应用，属于中档题．
练习册系列答案
相关题目
8．
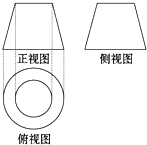如图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是（ ）
如图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是（ ）| A． | 6π | B． | 12π | C． | 18π | D． | 24π |
9．如图是一个空间几何体的三视图，则该几何体的全面积为（ ）
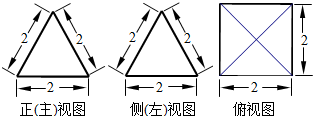
| A． | 12 | B． | 16 | C． | $\frac{{4\sqrt{3}}}{3}$+4 | D． | 4$\sqrt{3}$+4 |
13．如果cosα=$\frac{4}{5}$，那么$sin（α+\frac{π}{4}）-\frac{{\sqrt{2}}}{2}$cosα等于（ ）
| A． | $\frac{{2\sqrt{2}}}{5}$ | B． | ±$\frac{{2\sqrt{2}}}{5}$ | C． | $\frac{{3\sqrt{2}}}{10}$ | D． | ±$\frac{{3\sqrt{2}}}{10}$ |
3．用三段论推理：“对数函数y=logax（a＞0且a≠1）在（0，+∞）上是减函数，因为y=log2x是对数函数，所以y=log2x在（0，+∞）上是减函数”，你认为这个推理（ ）
| A． | 大前提错误 | B． | 小前提错误 | ||
| C． | 推理形式错误 | D． | 大前提和小前提都错误 |
10．设f（x）是定义在R上的偶函数，对任意x∈R，都有f（x-1）=f（x+1），且当x∈[0，1]时，f（x）=1-3x，若在区间[-6，6]内关于x的方程f（x）-loga（x+3）=0（0＜a＜1）恰有5个不同的实数根，则a的取值范围是（ ）
| A． | $（\frac{{\sqrt{6}}}{6}，\frac{1}{2}）$ | B． | $（\frac{{\sqrt{6}}}{6}，1）$ | C． | $（\frac{1}{2}，1）$ | D． | $（\frac{1}{2}，+∞）$ |