题目内容
15.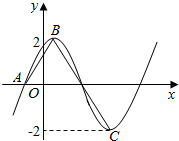 已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点.若f(0)=$\sqrt{3}$,
已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点.若f(0)=$\sqrt{3}$,且$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8.则f(x)的解析式为( )
| A. | f(x)=2sin(2x+$\frac{π}{3}$) | B. | f(x)=2sin(2x+$\frac{π}{6}$) | C. | f(x)=2sin(3x+$\frac{π}{3}$) | D. | f(x)=2sin(3x+$\frac{π}{6}$) |
分析 由图可设A(a,0),函数f(x)=2sin(ωx+φ)的周期为T,则B(a+$\frac{T}{4}$,2),C(a+$\frac{3T}{4}$,-2),易求$\overrightarrow{AB}$=($\frac{T}{4}$,2),$\overrightarrow{BC}$=($\frac{T}{2}$,-4),利用向量的坐标运算,将已知$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8坐标化整理,可求得T,从而可得ω的值,由f(0)=2sinφ=$\sqrt{3}$,又|φ|$<\frac{π}{2}$,从而可解得φ的值,即可解得f(x)的解析式.
解答 解:设A(a,0),函数f(x)=2sin(ωx+φ)的周期为T,则B(a+$\frac{T}{4}$,2),C(a+$\frac{3T}{4}$,-2),
∴$\overrightarrow{AB}$=($\frac{T}{4}$,2),$\overrightarrow{BC}$=($\frac{T}{2}$,-4),
∵$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8,
∴$\frac{{T}^{2}}{8}$-8=$\frac{{π}^{2}}{8}$-8,
整理得:T2=π2,
∴T=π,
解得:ω=$\frac{2π}{π}$=2,故有:f(x)=2sin(2x+φ),
∵f(0)=2sinφ=$\sqrt{3}$,可得sinφ=$\frac{\sqrt{3}}{2}$,又|φ|$<\frac{π}{2}$,解得:φ=$\frac{π}{3}$.
∴f(x)的解析式为:2sin(2x+$\frac{π}{3}$).
故选:A.
点评 本题考查函数y=Asin(ωx+φ)的图象解析式的确定,着重考查向量的数量积的坐标运算及其应用,属于中档题.

| A. | 5 | B. | ±$\sqrt{10}$ | C. | $\sqrt{10}$ | D. | -5 |
| A. | 0 | B. | 2 | C. | 4 | D. | 8 |
| x | 3 | 4 | 5 | 6 | 7 |
| y | 5.8 | 8.2 | 9.7 | 12.2 | 14.1 |
(2)判断变量x与y之间是正相关还是负相关,并估计产量为20吨时,生产能耗为多少吨标准煤?
参考数值:3×5.8+4×8.2+5×9.7+6×12.2+7×14.1=270.6.
| A. | -1 | B. | $\sqrt{3}$ | C. | 1 | D. | -$\sqrt{3}$ |
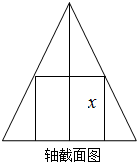 一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱:
一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱: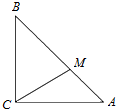 如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,
如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,